Radial Propagation Outgoing: Spherical Hankel Functions
The outgoing sound pressure waves in the solutions of the wave-equation in spherical coordinates are described by spherical harmonics and spherical Hankel functions, as so called "singular solutions" S(r,phi,theta)=hn(kr)*Ynm(phi,theta). These are travelling waves with a singularity at r=0 and have to fulfill the Sommerfeld radiation condition at r=infinity, i.e. p=-i*v. In the figure below, an animation of these functions is given for modes of the orders n=0...3. Their derivative h'n(kr) divided by i stands for the radial velicity.
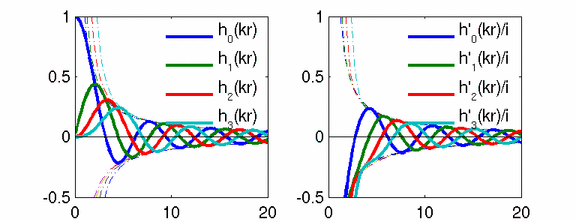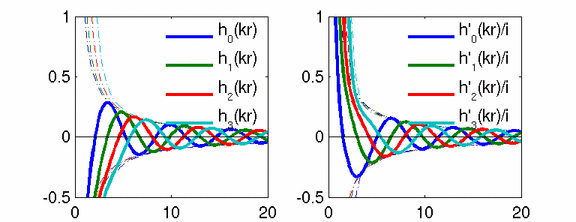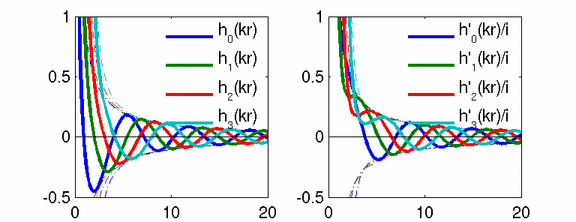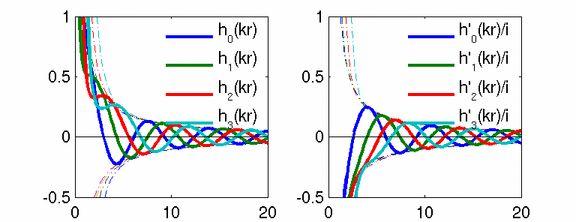
Franz Zotter, 2008.

