thermenface - Ein berührungsloses Interface zur Steuerung von Langzeitinstallationen
institut für elektronische musik und akustik
- Anforderungen
-
das Theremin
-
Ansatz
- Aufstellung der Theremine
-
Realisierung thermenface
- Frequenzmessung getfrequency
- automatische Kalibrierung autocalibrate
- Positionsberechnung getdistance
- About this document ...
Anforderungen Interaktive und reaktive System benötigen Input-Interfaces, mit denen BenutzerInnen mit ihnen in Verbindung treten könne.
Zur Kontrolle einer eindimensionalen Variablen (zum Beispiel Lautstärke oder Position auf einer Geraden) können dabei eine Vielzahl von Geräten wie Schieberegler und dergleichen eingesetzt werden. Bei all diesen Interfaces tritten die BenutzerInnen in ein mechanisch-haptisches Verhältnis zum System. Dies kann aus ästhetischen oder technischen Gründen nicht erwünscht sein. Es war daher ein Interface zu entwickeln, dass eine berührungslose Steuerung eines Parameters erlaubt. Ein solches Steuerinterface muß
- automatisch festellen, ob es gerade benutzt wird
- verläßlich den gesteuerten Parameter zurückgeben
Auch soll die Erscheinung des Interfaces sozusagen ``berührungslos'' sein, und die Benutzerin nicht in der Rezension beeinträchtigen.
Auf die Verwendung von Bilderkennung wurde in diesem Zusammenhang verzichtet, da sie einerseits rechenintensiv ist, andererseits von Parametern wie guter Ausleuchtung und kontrastreichen Bildern abhängig ist, die vor allem bei Klanginstallationen (dunkle Räume) nicht garantiert werden können.
das Theremin
Das ``Theremin'' 1 war (und ist) das erste Elektronische Musikinstrument der Geschichte, benannt nach seinem Erfinder Lew Termen.
Die Besonderheit des Theremins gegenüber anderen (herkömmlichen) Instrumenten ist, dass es nicht mechanisch-haptisch gesteurt wird, wie zum Beispiel durch Drücken einer Taste oder Streichen mit einem Bogen über eine Seite, sondern nur durch die Position (zum Beispiel einer Hand) relativ zu einem Fixpunkt im Raum (einer Antenne).
Dadurch ist das Theremin nicht nur als Musikinstrument interessant, sondern kann auch als Positionsdetektor (und in weiterer Folge als Bewegungsdetektor) verwendet werden. Tatsächlich hat es unter Stalin Pläne gegeben, die sowjetische Grenze mit Hilfe von Thereminen zu überwachen.
Herkömmliche Theremine verfügen über zwei orthogonale Antennen, wodurch sich unabhängig Lautstärke und Tonhöhe steuern lassen. Im Rahmen des ``berührungslosen Interfaces mit Theremin-Sensoren'' wurde allerdings mit fixer Lautstärke gearbeitet. Dadurch läßt sich sehr einfach feststellen, ob die Sensoren arbeiten (Signal über einem gewissen Pegel liegt an) oder nicht.
Hardware Technisch ist das Theremin ein Schwebungssummer, bei dem zwei hochfrequente Oszillatoren überlagert werden, wobei die Frequenz des einen Oszillators fix ist, während die Frequenz des anderen Oszillators über einen variablen Schwingkreis eingestellt werden kann. Die Kapazität des Schwingkreises wird dabei (teilweise) von Antenne und Spieler gebildet. Durch den Abstand von Antenne zur Spielerhand kann diese Kapazität verändert werden, wodurch sich die Resonanzfrequenz des Schwingkreises ändert.
Ansatz
Frequenz->Entfernung
Die Resonanzfrequenz eines passiven Schwingkreises kann angenähert
werden mit
| (1) |
Für Kugelkondensatoren gilt idealerweise
| (2) |
Der Schwebungssummer bildet die Differenzfrequenz der beiden Schwingkreise
| (3) |
Ein Kugelkondensator nähert das tatsächliche Verhalten eines Theremins nur an. Mangels einer geschlossenen Lösung lassen sich die obigen Gleichungen vereinfachen zu:
Jeder Entfernung von der Antenne kann also eindeutig eine Frequenz zugeordnet werden und umgekehrt.
Die Faktoren ![]() und
und ![]() können berechnet werden, indem man die Frequenzen
können berechnet werden, indem man die Frequenzen ![]() und
und ![]() an zwei bekannten Punkten (Abstände
an zwei bekannten Punkten (Abstände ![]() und
und ![]() ) mißt. Ist auch
) mißt. Ist auch ![]() unbekannt, so ist noch eine dritte Messung erforderlich.
unbekannt, so ist noch eine dritte Messung erforderlich.
In der Praxis ist es im Allgemeinen problematisch ``große'' Entfernungen zu detektieren, da die Frequenzänderung mit der Entfernung sehr klein wird.
Frequenzmessung Der Tongenerator eines Theremins ist als Schwebungssummer ausgeführt. Neben dem hörbaren tieffrequenten Anteil
Diese hohen Frequenzanteile werden bei der analog-digital Konversion herausgefiltert und stören daher das digital vorliegende Signal nicht.
Auftretende Seitenschwingungen sind so gering, dass die Frequenz des Oszillators mit einem einfachen Nulldurchgangsdetektor ermittelt werden kann.
| (8) |
Entfernung->Position Durch die Messung der Frequenz kann also der Abstand eines Körpers von der Antenne gemessen werden. Mißt man die Entfernung von zwei Fixpunkten, so kann daraus die Position des Körpers (im 2D-Fall) berechnet werden.
Die Position ![]() berechnet sich aus den Abständen
berechnet sich aus den Abständen ![]() und
und ![]() von den Antennen auf
von den Antennen auf ![]() und
und ![]() mit
mit
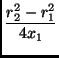
|
(9) | ||
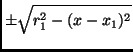
|
(10) | ||
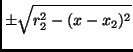
|
(11) |
Die y-Position ist also nicht eindeutig, da dass Vorzeichen nicht bestimmt werden kann.
Theoretisch kann also mit zwei Sensoren die Position eines Objektes (einer Hand) in einer Ebene bis auf ein Vorzeichen bestimmt werden.
Einschränkungen in der Praxis Durch konstruktive Maßnahmen (geerdete Abschirmung) läßt sich die Empfindlichkeit der Theremine von ``hinten'' (also der dem gegenüberliegenden Theremin abgewandten Seite) minimieren. Durch diese Richtcharakteristik läßt sich der Einfluss der Abstände zu den Antennen auf die Positionsberechnung linearisieren. Dadurch gilt :
Da die Frequenzänderung bei größeren Entfernungen sehr klein wird, kann es unmöglich sein, über den gesamten Bereich zwischen zwei Sensoren von beiden Sensoren verläßliche Daten zu erhalten.
Da kleine Entfernungen verläßlicher detektiert werden, ist es sinnvoll, die genauere (kleinere) Entfernung stärker in die Positionsberechnung einfließen zu lassen.
Gilt Gl. (
12
), so ist ![]() . Im Allgemeinen gilt jedoch Gl. (
12
) nicht, und
. Im Allgemeinen gilt jedoch Gl. (
12
) nicht, und ![]() bzw.
bzw. ![]() liefert jeweils die bessere Näherung an das Ergebnis.
liefert jeweils die bessere Näherung an das Ergebnis.
Problematisch ist hier nur der Übergang von ![]() auf
auf ![]() , da er bei großen Meßfehlern nicht stetig verlaufen muss und
die Position daher springen kann.
, da er bei großen Meßfehlern nicht stetig verlaufen muss und
die Position daher springen kann.
Durch Interpolation zwischen den ![]() und
und ![]() über ein Übergangsstück
über ein Übergangsstück ![]() , läßt sich diese Unstetigkeit beseitigen.
, läßt sich diese Unstetigkeit beseitigen.
| (15) |
Aufstellung der Theremine
Zwei Theremine werden ``genügend nahe'' nebeneinander an den Positionen
A und B aufgestellt. ``Genügend nahe'' bedeutet, dass, wenn sich eine
Hand an Position B um den geringsten noch zu detektierenden Betrag bewegt,
die Frequenz an Position A sich um mindestens ![]() Hz ändern muss.
Hz ändern muss.
``Genügend nahe'' ist also stark von der gewünschten Positionsauflösung und den verwendeten Thereminsensoren abhängig.
Realisierung thermenface (s. Abb. 3 )
Das thermenface liest die ersten beiden Kanäle der Soundkarte und interpretiert sie als die von den beiden Thereminsensoren generierten Signale.
Temperaturdrift und andere Störfaktoren
hermodrift Theremine sind stark temperaturabhängig. Dadurch behalten die nach Gl. ( 6 , 7 ) gewonnen Faktoren nur eine relativ kurze Zeit ihre Gültigkeit, danach müssen neue Messungen durchgeführt und daraus neue Faktoren gewonnen werden.Im Allgemeinen kann man jedoch nicht fortwährend Calibrierungs-Messungen
durchführen. Es ist daher notwendig, durch automatische Calibrierungsroutinen
immer aktuelle Faktoren ![]() und
und ![]() zu berechnen.
zu berechnen.
Frequenzmessung getfrequency (s. Abb. 4 )
Der Patch getfrequency führt die Frequenzmessung für
einen Kanal durch. Jedesmal, wenn er an seinem Eingang getriggert wird,
gibt er eine Liste aus, die die Frequenz ![]() des Signales und die Differenz
des Signales und die Differenz ![]() zur Ruhefrequenz enthält. Die Ruhefrequenz
zur Ruhefrequenz enthält. Die Ruhefrequenz ![]() ist jene Frequenz, die generiert wird, wenn sich keine Hand in der Nähe
der Theremine befindet (die Hand also ``unendlich weit'' entfernt ist).
ist jene Frequenz, die generiert wird, wenn sich keine Hand in der Nähe
der Theremine befindet (die Hand also ``unendlich weit'' entfernt ist).
Dem Patch werden zwei Argumente übergeben:
- <snd_channel>: der Kanal der Soundkarte, von dem gelesen werden soll
- <theremin-id>: der ``Name'' des Theremins
getfreq (s. Abb. 5 a)
Hier wird die eigentliche Frequenzmessung durchgeführt.
Zuerst wird in einem Hochpass ein allfälliger Gleichspannungsanteil entfernt. Mit dfreq~ wird durch Nullstellendetektion eine Grundfrequenzmessung durchgeführt, deren Ergebnis gemittelt wird. Nur wenn der Pegel des Eingangssignales höher als ein Schwellwert (default=60) ist, wird das Ergebnis über den Outlet ausgegeben.
driftguard (s. Abb. 5 b)
Da Thereminsensoren einer starken Temperaturdrift unterworfen sind, wird
hier versucht, diese zu detektieren. Dazu wird die Ruhefrequenz ![]() beobachtet.
beobachtet.
driftguard detektiert ![]() auf zwei verschiedene Arten:
auf zwei verschiedene Arten:
- watch lowest: Durch das indirekt-proportionale Verhältnis
von Frequenz und Entfernung ist
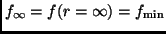 . Unterschreitet die aktuelle Frequenz
. Unterschreitet die aktuelle Frequenz 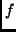 die bisherige
die bisherige 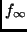 , so wird
, so wird 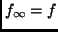 . Danach wird
. Danach wird 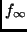 langsam wieder exponentiell inkremeniert.
langsam wieder exponentiell inkremeniert.
- watch change: Bei großen Temperaturdriften der Frequenz
nach oben, könnte es zu lange dauern, bis die obengenannte Methode
sich auf die tatsächliche
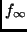 einstellt. Daher wird zusätzlich die Frequenzänderung beobachtet.
Bleibt
einstellt. Daher wird zusätzlich die Frequenzänderung beobachtet.
Bleibt 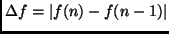 eine genügend lange Zeit finf_time (in Sekunden) durchgehend
unter einem Schwellwert delta_finf, so wird ein Mittelwert als
neue Ruhefrequenz
eine genügend lange Zeit finf_time (in Sekunden) durchgehend
unter einem Schwellwert delta_finf, so wird ein Mittelwert als
neue Ruhefrequenz 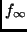 eingestellt.
eingestellt.
driftguard gibt eine Liste aus, die neben der aktuellen Frequenz
auch die Differenz ![]() und die Ruhefrequenz
und die Ruhefrequenz ![]() enthält.
enthält.
automatische Kalibrierung autocalibrate (s. Abb. 6 )
Durch die Temperaturdrift ist es notwendig, die Koeffizienten ![]() und
und ![]() immer wieder zu aktualisieren.
immer wieder zu aktualisieren.
Greift man bei einem Theremin direkt auf die Antenne, so geht die Frequenz
![]() . So hohe Frequenzen können jedoch nicht in die digitale Domäne
überführt werden (zumindest nicht bei herkömmlichen Audioabtastraten
von
. So hohe Frequenzen können jedoch nicht in die digitale Domäne
überführt werden (zumindest nicht bei herkömmlichen Audioabtastraten
von ![]() kHz). Durch geeignete Abschirmung der Antennte kann es aber unmöglich
gemacht werden, direkt die Antenne zu berühren und die maximal generierte
Frequenz auf unter 20kHz zu begrenzen.
kHz). Durch geeignete Abschirmung der Antennte kann es aber unmöglich
gemacht werden, direkt die Antenne zu berühren und die maximal generierte
Frequenz auf unter 20kHz zu begrenzen.
Die maximale Frequenz ![]() tritt dann auf, wenn die Benutzerin ihre Hand in minimalem Abstand
tritt dann auf, wenn die Benutzerin ihre Hand in minimalem Abstand ![]() von der Antenne positioniert.
von der Antenne positioniert.
autocal (s. Abb. 7 (a))
Die Ausgangsfrequenz des Theremins wird beobachtet und ihr Maximal- und
Minimalwert ermittelt. ![]() wird dem Minimalabstand
wird dem Minimalabstand ![]() zugeordnet. Der Wert
zugeordnet. Der Wert ![]() nimmt exponentiell ab, so nicht eine neue Maximalfrequenz eingelesen wird.
nimmt exponentiell ab, so nicht eine neue Maximalfrequenz eingelesen wird.
Der gemessene Minimalewert wird um ``ein bisschen'' (um den Skalierungsfaktor
fmin_faktor) vergrößert, sodass ![]() nicht mehr gleich der Ruhefrequenz (mit
nicht mehr gleich der Ruhefrequenz (mit ![]() ) ist, sondern eher dem ``Maximal''
2
-Abstand
) ist, sondern eher dem ``Maximal''
2
-Abstand ![]() entspricht. Der Wert
entspricht. Der Wert ![]() nimmt exponentiell zu, so nicht eine neue Minimalfrequenz eingelesen wird.
(s. Abb.
7
(b) und
8
)
nimmt exponentiell zu, so nicht eine neue Minimalfrequenz eingelesen wird.
(s. Abb.
7
(b) und
8
)
Durch Beobachtung der Grundfrequenz des Signales lassen sich also Schätzwerte
für ![]() und
und ![]() bestimmen. Ändern sich diese ``Kalibrierugsfrequenzen'', so werden
nach Gl. (
6
,
7
) in calccoeff neue Faktoren berechnet. Diese werden über
cal_coeff zum Objekt f2d geschickt, wo die Frequenz->Entfernungs-Transformation
durchgeführt wird.
bestimmen. Ändern sich diese ``Kalibrierugsfrequenzen'', so werden
nach Gl. (
6
,
7
) in calccoeff neue Faktoren berechnet. Diese werden über
cal_coeff zum Objekt f2d geschickt, wo die Frequenz->Entfernungs-Transformation
durchgeführt wird.
Positionsberechnung getdistance (s. Abb. 9 )
Es muss zuerst überprüft werden, ob überhaupt eine Hand im Bereich der Sensoren detektiert wird, und ob sie sich in einer ``sinnvollen'' Position 3 befindet.
Sollte dies der Fall sein, so wird eine Liste ausgegeben, die die Handposition und ein gesetztes valid-flag beinhaltet. Wird keine Hand innerhalb des Gültigkeitsbereiches detektiert, so wird das valid-flag auf 0 zurückgesetzt, und mit der letzten gültigen Position ausgegeben.
checkhand (s. Abb. 10 (a))
Beinflusst keine Hand die Thereminsensoren, so liefern beide Sensoren
ein Signal mit der jeweiligen Ruhefrequenz ![]() 4
.
4
.
Übersteigt die Differenz zwischen berechneter Ruhefrequenz (s. 5.1.2 ) und tatsächlich gemessener Frequenz einen Schwellewert delta_finf , so wird angenommen, dass eine Hand detektiert wurde.
Am ersten Outlet wird eine Liste mit den beiden Thereminfrequenzen ausgegeben, am zweiten Outlet wird angezeigt, ob eine Hand detektiert worden ist.
f2d (s. Abb. 11 (a))
Nach Gl. ( 5 ) wird hier mit den in autocal gewonnen Faktoren die Frequenz->Entfernungs-Transformation vorgenommen.
Liegt keine gültige Frequenz an (f=0), so wird 0 ausgegeben.
checkvalidist (s. Abb. 10 (b))
Hier wird überprüft ,ob die mit f2d (s. 5.3.2 ) gewonnene Entfernung innerhalb des Gültigkeitsbereiches liegt. Es wird ein korrigierter, also auf den Gültigkeitsbereich begrenzter Wert ausgegeben, und ein valid-flag am zweiten Outlet gesetzt.
dist2coord (s. Abb. 11 (b))
Ist zumindest ein Theremin aktiv (also die detektierte Entfernung innerhalb
des Gültigkeitsbereiches) so wird hier aus den beiden Entfernungen
nach Gl. (
13
-
16
) die Handposition berechnet. Um von der tatsächlichen Aufstellung
möglichst unabhängig zu sein, wird die Entfernung ![]() zwischen den beiden Sensoren herausgerechnet. Da durch die Mittelung (Gl.
16
) nicht der volle Wertebereich zwischen -1 und +1 ausgeschöpft wird,
kann der Wertebereich, den die gemessene Handposition annehmen kann, nötigenfalls
mit einem Spreizungsfaktor spreizung aufgedehnt werden. Die endgültige
Position wird jedenfalls auf den Bereich
zwischen den beiden Sensoren herausgerechnet. Da durch die Mittelung (Gl.
16
) nicht der volle Wertebereich zwischen -1 und +1 ausgeschöpft wird,
kann der Wertebereich, den die gemessene Handposition annehmen kann, nötigenfalls
mit einem Spreizungsfaktor spreizung aufgedehnt werden. Die endgültige
Position wird jedenfalls auf den Bereich ![]() begrenzt.
begrenzt.
Gegebenenfalls wird auch noch die Links-rechts-Orientierung umgedreht.
About this document ... thermenface
Ein berührungsloses Interface zur Steuerung von Langzeitinstallationen
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos
, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore
, Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -dir /Net/iem/Benutzer/zmoelnig/public_html/publications/thermenface
theremin.tex
The translation was initiated by Johannes M Zmoelnig on 2001-10-17
Footnotes
- ... ``Theremin'' 1
- auch ``Ätherophon'' oder ``Termenvox'' genannt
- ... ``Maximal'' 2
- Maximal im Sinne von ``größtmöglicher Abstand, bei dem noch ein Frequenzänderung detektierbar ist''
- ... Position 3
- ``nicht sinnvolle'' Positionen sind
- Abstände von Sensoren
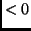 (durch Störungen, für die die berechneten Faktoren
(durch Störungen, für die die berechneten Faktoren 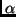 und
und 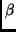 falsche Werte liefern)
falsche Werte liefern) - Positionen außerhalb des erwünschten Bereiches
- Abstände von Sensoren
- ...
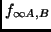 4
4
- Wobei im allgemeinen durch Bauteilstreuungen,...gilt
Johannes M Zmoelnig 2001-10-17
© 2000, zuletzt geändert am 17. Oktober 2001.
Resources
| Titel | Beschreibung |
|---|---|
| thermenface_zmoelnig-Dateien |


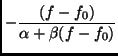
![\includegraphics[scale=0.7]{r2f.eps}](thermenface_zmoelnig-Dateien/img17.png)
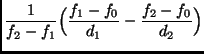
![\includegraphics[scale=0.35]{d2p.eps}](thermenface_zmoelnig-Dateien/img36.png)
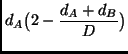
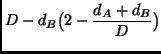
![\includegraphics[scale=0.7]{thermenface.eps}](thermenface_zmoelnig-Dateien/img53.png)
![\includegraphics[scale=0.7]{getfrequency.eps}](thermenface_zmoelnig-Dateien/img57.png)
![\includegraphics[scale=0.7]{getfreq.eps}](thermenface_zmoelnig-Dateien/img58.png)
![\includegraphics[scale=0.7]{driftguard.eps}](thermenface_zmoelnig-Dateien/img59.png)
![\includegraphics[scale=0.7]{autocalibrate.eps}](thermenface_zmoelnig-Dateien/img67.png)
![\includegraphics[scale=0.7]{autocal.eps}](thermenface_zmoelnig-Dateien/img69.png)
![\includegraphics[scale=0.7]{cal-minmax.eps}](thermenface_zmoelnig-Dateien/img70.png)
![\includegraphics[scale=0.7]{newmin.eps}](thermenface_zmoelnig-Dateien/img76.png)
![\includegraphics[scale=0.7]{newmax.eps}](thermenface_zmoelnig-Dateien/img77.png)
![\includegraphics[scale=0.7]{getdistance.eps}](thermenface_zmoelnig-Dateien/img79.png)
![\includegraphics[scale=0.7]{checkhand.eps}](thermenface_zmoelnig-Dateien/img82.png)
![\includegraphics[scale=0.7]{checkvalidist.eps}](thermenface_zmoelnig-Dateien/img83.png)
![\includegraphics[scale=0.7]{f2d.eps}](thermenface_zmoelnig-Dateien/img84.png)
![\includegraphics[scale=0.7]{dist2coord.eps}](thermenface_zmoelnig-Dateien/img85.png)