WaveTabShaper
Inhaltsverzeichnis
- Allgemeines
- Installation von Wave TabShaper
- Starten von Wave TabShaper
- Arbeiten mit Wave TabShaper
4.1 Sounds öffnen und speichern
4.2 Waveshaping
4.3 Fourier Synthesis
4.4 Mathematical Calculation
4.5 Manual Editing - Die Kommunikation zwischen Wave TabShaper und MAX
- Beispiele
- Theoretische Abhandlung von Waveshaping
- Anhang
1. Allgemeines
Dieses Programm wurde amINSTITUT FÜR ELEKTRONISCHE MUSIK
AN DER UNIVERSITÄT FÜR MUSIK UND DARSTELLENDE KUNST IN GRAZ
Jakoministr. 3 - 5, A - 8010 Graz, Austria
geschrieben.
Konzeption: Winfried Ritsch und Thomas Musil
Programmierung: Thomas Musil (email: musil@iem.kug.ac.at)
WaveTabShaper ist ein Wavetable-Editor, mit dem Sie 512 Samples lange Soundfiles ( Wavetables ) bearbeiten bzw. generieren
können. WaveTabShaper kommuniziert optional mit einem grafisch bedienbaren Echtzeit-Klangverarbeitungs-Programm namens MAX, vorausgesetzt
Sie besitzen dazu eine ISPW-Karte (Ircam Signal Processing Workstation).
Die mittels WaveTabShaper generierten Soundfiles können Sie in ein Oszillator-Objekt "osc1~" laden.
"osc1~" erzeugt nun aus dieser Wavetable entweder eine periodische Schwingung, oder es verzerrt ein Signal anhand dieser
Wavetable-Kennlinie. Mit WaveTabShaper können Sie auch Wavetables in Echtzeit entwickeln, indem Sie statt dem "osc1~"-Objekt
entsprechend programmierte Externals verwenden.
waveshape2~ , waveshape4~: das sind 2 Verzerrungs-Prozessoren mit 2-Punt- bzw. 4-Punkt-Interpolation;
oscillator2~, oscillator2_I~ : das sind 2 Wavetable-Oszillatoren mit 2-Punt-Interpolation.
2. Installation von WaveTabShaper
Zuerst kopieren Sie das Paket "WaveTabShaper.compressed" in einen Ordner, wo sich auch andere Sound-Tools befinden. Dann klicken Sie dieses Paket an und dekomprimieren es (Workspace->File->Decompress. Der nun entstandene Ordner "WaveTabShaper" soll enthalten:- einen Ordner names "Documentation",
- einen Ordner names "MaxPatches",
- die Applikation "WaveTabShaper.app",
- und das Icon ".dir.tiff".
In "MaxPatches" finden Sie den Ordner "sounds" (mit einigen vorgefertigten Wavetables ) und den Ordner "wavelib" (Bibliothek von MAX-Objekte für WaveTabShaper .
3. Starten von WaveTabShaper
Folgende 3 Möglichkeiten stehen Ihnen zur Verfügung, das Programm WaveTabShaper in Betrieb zu nehmen:- Falls Sie eine ISPW-Karte besitzen, starten Sie das Programm "Max.app" und öffnen den Patch "WaveShape2.pat
" in "MaxPatches".
Anschließend starten Sie "WaveTabShaper.app", es erscheint nun die Arbeitsoberfläche von WaveTabShaper und nach ca. 4 Sekunden die Mitteilung, daß der Kommunikations-Kanal zwischen MAX und WaveTabShaper geöffnet wurde.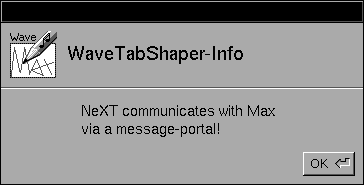
Nachdem Sie "OK" angeklickt haben, erscheint in der untersten Zeile des MAX-Konsole-Fensters die Nachricht "(1): print: WaveTabShaper has been started!". Sie brauchen nur mehr im Patch "WaveShape2.pat" die Message-Box ";max dsp 1" anzuklicken und die 3 Sliders aufzuziehen.
Ab diesem Zeitpunkt können Sie in WaveTabShaper (Betriebsart WaveShaping Ihre gewünschten Oberwellen-Anteile einstellen und anhören. - Falls Sie eine ISPW-Karte besitzen und das Programm "Max.app" läuft noch nicht, starten Sie das Programm
"WaveTabShaper.app". Es erscheint nun die Arbeitsoberfläche von WaveTabShaper und diese Warnung, daß das
Programm "Max.app" noch nicht gestartet wurde.
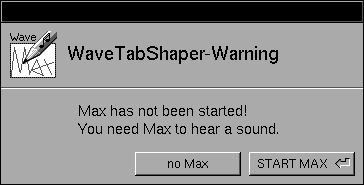
Sie können nun auf "START MAX" klicken, und WaveTabShaper startet für Sie die MAX-Applikation samt dem Patch "WaveShape2.pat". Nach ca. 6 Sekunden erscheint die Mitteilung, daß der Kommunikations-Kanal zwischen MAX und WaveTabShaper geöffnet wurde.
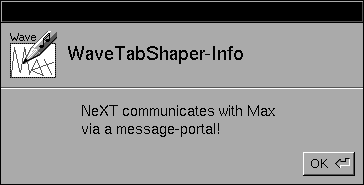
Nachdem Sie "OK" angeklickt haben, verfahren Sie wie unter 1.).
- Falls Sie keine ISPW-Karte besitzen, starten Sie das Programm "WaveTabShaper.app". Es erscheint nun die Arbeitsoberfläche von
WaveTabShaper und diese Warnung, daß das Programm Max.app noch nicht gestartet wurde.
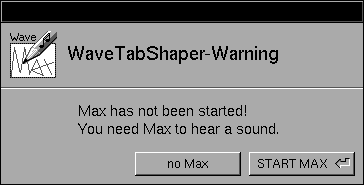
Hier sollen Sie nur auf "no Max" klicken, und WaveTabShaper arbeitet nur als grafische Applikation.
4. Arbeiten mit WaveTabShaper
Im obersten Bereich der Arbeitsoberfläche befindet sich ein Pop-Up-Menü. Mit Hilfe dieses Pop-Up-Menüs können Sie eine der folgenden 4 Betriebsarten von WaveTabShaper auswählen:
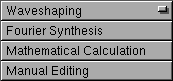
Waveshaping dient ausschließlich zur Verzerrung eines Signals.
Fourier Synthesis dient ausschließlich zur Erzeugung eines periodischen Signals.
Mathematical Calculation und Manual Editing können Sie sowohl zur Erzeugung von periodischen Signalen (Oszillatoren) als auch zur Erzeugung
aperiodischer Signale (Hüllkurven), sowie zur Verzerrung von Signalen heranziehen.
Da jede Betriebsart über einen eigenen Wavetable-Speicher verfügt, können Sie beliebig zwischen den Betriebsarten wechseln, ohne die in anderen
Betriebsarten erstellten Wavetables zu löschen. Sobald Sie die Betriebsart gewechselt haben, wird die aktuelle Wavetable
optional in das MAX-Extrernal-Objekt übertragen.
Im Hauptmenü von WaveTabShaper finden Sie in der ersten Zeile den Eintrag "Info".
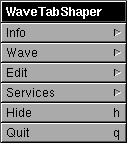
Im Eintrag "Info Panel" werden Sie über die Urheberrechte bzw. über die E-Mail-Adresse des Instituts informiert. Im Eintrag "About WaveTabShaper" finden Sie den gesamten Hilfe-Text.
Der Eintrag "Edit" des Hauptmenüs bietet Ihnen Kopier-Funktionen für Text-Felder.
Abschließend gibt es noch die Einträge "Hide" und "Quit" zum Verstecken bzw. zum Beenden des Programms.
4.1 Sounds öffnen und speichern
Hinter dem Hauptmenü-Eintrag "Wave" finden Sie die beiden Einträge "Open..." und "Save As...".
Wenn Sie den Eintrag "Save As..." anklicken, öffnet sich ein Save-Panel, mit dessen Hilfe Sie die momentan angezeigte Wavetable als Soundfile speichern können ( wavename.snd ). In Abhängikeit der gewählten Betriebsart wird noch ein zweites File mit Zusatz-Information gespeichert (In den Betribsarten Waveshaping und Fourier Synthesis wird die angezeigte Liste als ASCII-File gespeichert, in der Betriebsart Mathematical Calculation werden die beiden Grenzen in x-Richtung gespeichert, in der Betriebsart Manual Editing wird kein Zusatz-File gespeichert).
MAX unterscheidet 2 Arten von Soundfiles (Wavetables ), die das Max-Objekt "osc1~" laden kann:
"filename.snd" und "nowrap-filename.snd". Beide Wavetables haben eine Länge von 512 Samples. Die erste Art wird
für Wavetables verwendet, die periodisch stetige Verläufe aufweisen, die zweite Art wird verwendet für Wavetables, die eine Unstetigkeit
(Sprung in der Amplitude) zwischen 512. und 1. Sample aufweisen.
Diese Unstetigkeit wird auch bei langsamen Durchlaufen der Wavetable immer als senkrechter Sprung beibehalten ( "osc1~" verwendet
eine 2-Punkt-Interpolation). Unter den Betriebsarten Waveshaping und Fourier Synthesis ist es sinnvoll, die Wavtables als normale Soundfiles
zu speichern; unter den Betriebsarten Mathematical Calculation und Manual Editing kommt es darauf an, wie Sie diese Wavetables verwenden wollen.
Dient hier die Wavetable als Hüllkurve oder als Oszillator mit einer Unstetigkeit zwischen Beginn und Ende, sollen Sie sie auf jeden Fall mit dem
Präfix "nowrap-" speichern; dient sie als Verzerrungs-Kennlinie mit einer Unstetigkeit zwischen Beginn und Ende, speichern Sie sie auch mit dem
Präfix "nowrap-". In den beiden zuletzt genannten Betriebsarten bleibt nur mehr die Anwendung als Oszillator-Wavetable mit stetigen
Übergängen übrig, bei der Sie die Wavetable als normales Soundfile speichern können.
Wenn Sie "Open..." anklicken, öffnet sich ein Open-Panel, mit dessen Hilfe Sie ein Soundfile als Wavetable laden können. Diese Wavetable wird dann in der zugehörigen Betriebsart zur Anzeige gebracht.
4.2 Waveshaping
Im Waveshaping-Modus konstruieren Sie eine Wavetable, die als Verzerrungs-Kennliniedient. Ein MAX-Objekt (entweder osc1~ oder waveshape2~, waveshape4~) berechnet diese Verzerrung und formt ein sinusförmiges Eingangssignal mit der Amplitude von 1.0 in ein Ausgangssignal mit den gewünschten Oberwellen-Anteilen um (siehe Theorie). Die gewünschten Oberwellen-Anteile können Sie entweder mit den 3 Slidern (rechts) einstellen oder in die Liste (links) eintragen.
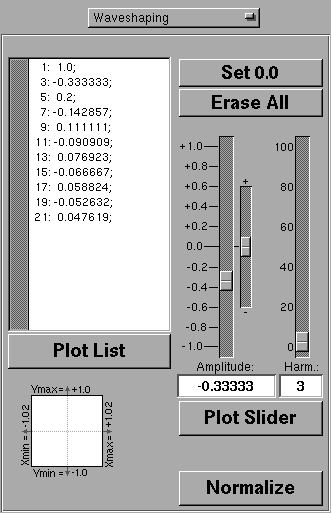
Mit diesem Slider können Sie die gewünschte Harmonische (von 0 bis 100) auswählen;
die genaue Zahl erscheint im Textfeld darunter darunter.
Daneben befinden sich 2 weitere Slider, mit denen Sie die Amplitude der gewählten Harmonischen einstellen können: Der größere dient zur Grobeinstellung von -1.0 bis +1.0 (mit einer Schrittweite von 0.01); der kleinere zur relativen Feinabstimmung von -0.0098 bis +0.0098 (mit einer Schrittweite von 0.0002 ). Im Textfeld darunter wird die Amplitude als Summe der beiden Slider angezeigt. Sie können den gewünschten Amplitudenwert aber auch direkt in dieses Textfeld eintragen.
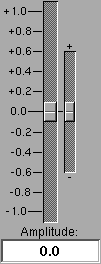
Sobald Sie den großen Slider neuerlich bewegen, wird der kleine Slider automatisch wieder in Null-Stellung gebracht.
Um den editierten Amplitudenwert zur jeweiligen Harmonischen in die Verzerrungs-Kennlinie zu übertragen, klicken Sie den Button "Plot Slider" an.

Dadurch bewirken Sie drei Dinge:
- Die graphische Kennlinie wird aktualisiert und neu angezeigt.
- Die Kennlinie wird optional in das MAX-External-Objekt übertragen.
- Der neue Amplitudenwert der Harmonischen wird in das Listen-Feld eingetragen.
Um die Amplitude einer Harmonischen genau auf 0.0 zu setzen, klicken Sie auf den Button "Set 0.0".
Wollen Sie die gesamte Verzerrungs-Kennlinie löschen, so klicken Sie auf den Button "Erase All".

Vorsicht: Diesen Schritt können Sie nicht mehr rückgängig machen!
Den gewünschten Oberwellen-Gehalt der Verzerrungs-Kennlinie können Sie auch direkt in die Liste eingeben. Dabei halten Sie sich an folgende Syntax:
- eine Ganzzahl (Harmonische)
- ein Doppelpunkt (zur Trennung)
- eine Gleitkommazahl (Amplitude)
- ein Strich-Punkt (Ende der Zeile)
Zur besseren Lesbarkeit können Sie auch Leer- und Return-Zeichen einfügen.
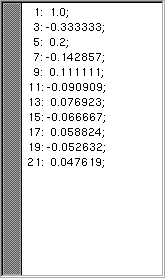
Dieses Beispiel erzeugt eine rechteckförmige Verzerrung eines Sinus-Signals mit beschränktem Oberwellengehalt (bis zur 21. Harmonischen).
Sobald Sie den Button "Plot List" anklicken, berechnet WaveTabShaper aus der eingegebenen Liste eine neue Kennlinie.

Genauso wie der Button "Plot Slider" bewirkt auch "Plot List" drei weitere Dinge:
- Die graphische Kennlinie wird aktualisiert und neu angezeigt.
- Die Kennlinie wird optional in das MAX-External-Objekt übertragen.
- Der Amplitudenwert des Sliders wird entsprechend korrigiert.
Begrenzungen:
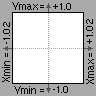
Die Grenzen der y-Richtung sind -1.0 und +1.0; die der x-Richtung zwischen -1.02 und +1.02. Würde man auch die x-Richtungs-Grenzen mit +/- 1.0 festlegen und die Verzerrungs-Kennlinie als i.) "filename.snd" bzw. als ii.) "nowrap-filename.snd" abspeichern, käme es bei höheren Harmonischen zu hörbaren Interpolations-Fehlern. Das MAX-Objekt osc1~ interpoliert zwischen den 512 Werten eines geladenen Soundfiles.
ad i):
Hier würde osc1~ zwischen dem 512. Sample und dem 1. Sample interpolieren. Das heißt, daß für die negative Halbwelle 256 Samples, für
die positive Halbwelle aber nur 255 Samples für eine fehlerfreie Interpolation zur Verfügung stehen.
ad ii):
osc1~ extrapoliert zwischen dem 512. Sample und dem 1. Sample die Interpolations-Funktion vom Wert des 511. und des 512. Sample. Dies führt bei höheren
Harmonischen zu hörbaren Rechenfehlern. Daher wurden die Kennlinien-Grenzen erweitert (-1.02 .... + 1.02), damit eine fehlerfreie Interpolation innerhalb der erlaubten
Grenzen ( -1.0 .... + 1.0 ) möglich ist.
Wenn die Kennlinie in y-Richtung über die Begrenzungswerte von -1.0 bzw. +1.0 hinausgeht oder diese stark unterschreitet, klicken Sie auf "Normalize".

Achtung: "Normalize" verändert auch die Amplituden-Werte in der Liste! Wenn Sie eine analytisch formulierbare Verzerrung weiter entwickeln wollen, sollten Sie die Verzerungs-Kennlinie speichern, bevor Sie diesen Befehl geben.
4.3 Fourier Synthesis
In diesem Modus können Sie die Sinus-bzw. Cosinus-Anteile einer Wavetable für eine Fourier-Synthese eingeben. Diese Wavetable wird dann im MAX-Objekt (entweder osc1~ oder oscillator2~, oscillator2_I~) zyklisch ausgelesen. Die gewünschten Harmonischen können Sie entweder mit den 5 Slidern (rechts) einstellen oder in die Liste (links) eintragen.
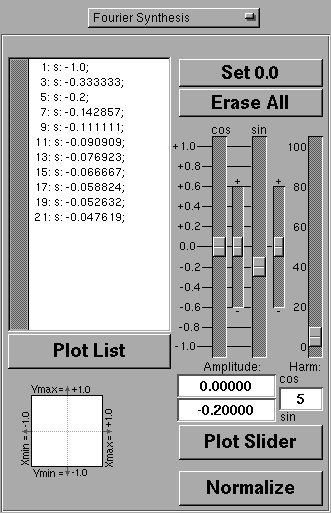
Mit diesem Slider können Sie die gewünschte Harmonische ( von 0 bis 100 ) auswählen;
die genaue Zahl erscheint im Textfeld darunter.
Daneben befinden sich 4 weitere Slider, mit denen Sie die Amplitude der gewählten Harmonischen einstellen können: Die beiden großen dienen zur Grobeinstellung der Sinus- bzw. Cosinus-Amplitude von -1.0 bis +1.0 (mit einer Schrittweite von 0.01); die beiden kleineren zur relativen Feinabstimmung von -0.0098 bis +0.0098 (mit einer Schrittweite von 0.0002 ). Im Textfeld darunter wird jeweils die Sinus- bzw. Cosinus-Amplitude als Summe der beiden Slider angezeigt. Sie können den gewünschten Amplitudenwert aber auch direkt in diese beiden Textfelder eintragen.
Sobald Sie einen der beiden großen Slider neuerlich bewegen, wird der dazugehörige kleine Slider automatisch wieder in Null-Stellung gebracht.
Um die beiden editierten Amplitudenwerte zur jeweiligen Harmonischen in die Wavetable zu übertragen, klicken Sie den Button "Plot Slider" an.

Dadurch bewirken Sie drei Dinge:
- Die graphische Wavetable wird aktualisiert und neu angezeigt.
- Die Wavetable wird optional in das MAX-External-Objekt übertragen.
- Der beiden neuen Amplitudenwerte der Harmonischen werden in das Listen-Feld eingetragen.
Um die beiden Amplitudenwerte einer Harmonischen genau auf 0.0 zu setzen, klicken Sie auf den Button "Set 0.0".
Es erfolgen die gleichen 3 Reaktionen wie beim Anklicken von "Plot Slider".
Wollen Sie die gesamte Verzerrungs-Kennlinie löschen, so klicken Sie auf den Button "Erase All".

Vorsicht: Diesen Schritt können Sie nicht mehr rückgängig machen!
Die gewünschten Harmonischen der Wavetable können Sie auch direkt in die Liste eingeben. Dabei halten Sie sich an folgende Syntax:
- Eine Ganz-Zahl (Harmonische)
- Ein Doppel-Punkt (zur Trennung)
- Ein "s" bzw. ein "c" (für Sinus bzw. Cosinus)
- Ein Doppel-Punkt (zur Trennung)
- Eine Gleit-Komma-Zahl (Amplitude)
- Ein Strich-Punkt (Ende der Zeile)
Zur besseren Lesbarkeit können Sie auch Leer- und Return-Zeichen einfügen.
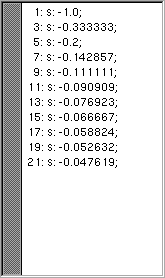
Dieses Beispiel erzeugt eine rechteckförmige Wavetable mit beschränktem Oberwellengehalt (bis zur 21. Harmonischen).
Sobald Sie den Button "Plot List" anklicken, berechnet WaveTabShaper aus der eingegebenen Liste eine neue Wavetable.

Genauso wie der Button "Plot Slider" bewirkt auch "Plot List" drei weitere Dinge:
- Die graphische Kennlinie wird aktualisiert und neu angezeigt.
- Die Kennlinie wird optional in das MAX-External-Objekt übertragen.
- Die Amplitudenwerte der Slider werden entsprechend korrigiert.
Begrenzungen:
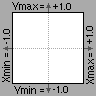
Die Grenzen der x- und der y-Richtung sind -1.0 und +1.0.
Wenn die Wavetable in y-Richtung über die Begrenzungswerte von -1.0 bzw. +1.0 hinausgeht oder diese stark unterschreitet, klicken Sie auf "Normalize".

Achtung: "Normalize" verändert auch die Amplituden-Werte in der Liste! Wenn Sie eine analytisch formulierbare Wavetable weiter entwickeln wollen, sollten Sie sie abspeichern, bevor Sie diesen Befehl geben.
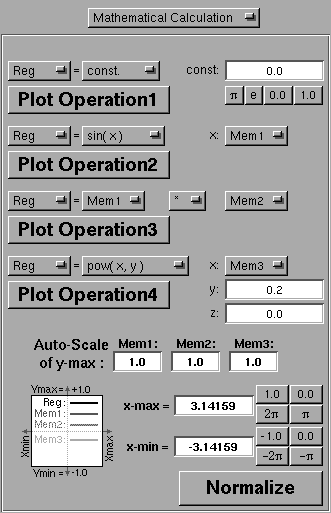
4.4 Mathematical Calculation
In diesem Modus können Sie Wavetables mit Hilfe mathematischer Operationen berechnen. Diese Operationen bzw. Zuweisungsvorschriften unterteilen sich in vier Bereiche:- Register initialisieren bzw. kopieren (Operation1)
- Operationen mit einem Register als Argument (Operation2)
- Operationen mit zwei Registern als Argumente (Operation3)
- Operationen mit einem Register und einer bzw. zwei Konstanten als Argumente (Operation4)
Außerdem besitzt Mathematical Calculation 4 Register (Wavetables):
Die 3 Register "Mem1", "Mem2" und "Mem3" können Sie als Hilfsregister verwenden; nur das Register
"Reg" können Sie speichern bzw. in ein MAX-External-Objekt übertragen.
4.4.1 Operation1

Mit diesem Pop-Up-Menü wählen Sie das Ergebnis-Register der Operation1:
Als Argument können Sie auswählen:
- eines der vier Register
- die "y = x"-Gleichung über den Bereich von x-min bis x-max
- eine Konstante Zahl über den Bereich von x-min bis x-max
- eines der drei Anzeige-Register der Betriebsarten Waveshaping, Fourier Synthesis bzw. Manual Editing
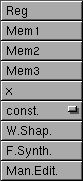
Die Konstante "const" können Sie mit 4 vordefinierten Werten belegen; Sie können den Wert aber auch direkt in das Textfeld eintragen.
Durch Anklicken des Buttons "Plot Operation1" bewirken Sie 3 Dinge:
- Das Ergebnis-Register wird laut Zuweisungs-Vorschrift berechnet.
- Die graphische Darstellung des Ergebnis-Registers wird aktualisiert und neu angezeigt.
- Falls Sie "Reg" als Ergebnisregister eingestellt haben, wird es optional in das MAX-External-Objekt übertragen.
4.4.2 Operation2

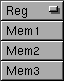
Das Ergebnis-Register der Operation2 wählen Sie wieder mit diesem Pop-Up-Menü:
Die gewünschte mathematische Funktion wählen Sie aus diesem Pop-Up-Menü:
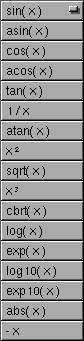
| sin( x ) | Sinus von Register x; |
| asin( x ) | ArcusSinus von Register x; |
| cos( x ) | Cosinus von Register x; |
| acos( x ) | ArcusCosinus von Register x; |
| tan( x ) | Tangens von Register x; |
| 1 / x | 1.0 dividiert durch Register x; |
| atan( x ) | ArcusTangens von Register x; |
| xý | Register x zum Quadrat; |
| sqrt( x ) | QuadratWurzel aus Register x; |
| xþ | Register x zur 3. Potenz; |
| cbrt( x ) | KubikWurzel aus Register x; |
| log( x ) | Logarithmus zur Basis e von Register x; |
| exp( x ) | e hoch Register x; |
| log10( x ) | Logarithmus zur Basis 10 von Register x; |
| exp10( x ) | 10.0 hoch Register x; |
| abs( x ) | Betrag von Register x; |
| - x | 0.0 minus Register x; |
Falls die Werte eines Wavetable-Registers die mathematisch definierten Grenzen eines Arguments verletzen, werden sie in, für die Berechnung erlaubte, Bereiche gesetzt.
(Beispiel: Die Quadratwurzel einer negativen Zahl wird 0 gesetzt.)
Das Argument "x" der Operation2 ist eines dieser vier Register:
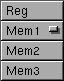
Indem Sie den Button "Plot Operation2" anklicken, bewirken Sie wieder die bereits bekannten 3 Dinge:
- Das Ergebnis-Register wird laut Zuweisungs-Vorschrift berechnet.
- Die graphische Darstellung des Ergebnis-Registers wird aktualisiert und neu angezeigt.
- Falls Sie "Reg" als Ergebnisregister eingestellt haben, wird es optional in das MAX-External-Objekt übertragen.
4.4.3 Operation3

Das Ergebnis-Register sowie das 1. und 2. Argument der Operation3 wählen Sie jeweils aus diesem Pop-Up-Menü:
Aus diesem Pop-Up-Menü wählen Sie eine der 4 Grundrechnungsarten:

Indem Sie den Button "Plot Operation3" anklicken, bewirken Sie wieder die bereits bekannten 3 Dinge:
- Das Ergebnis-Register wird laut Zuweisungs-Vorschrift berechnet.
- Die graphische Darstellung des Ergebnis-Registers wird aktualisiert und neu angezeigt.
- Falls Sie "Reg" als Ergebnisregister eingestellt haben, wird es optional in das MAX-External-Objekt übertragen.
4.4.4 Operation4
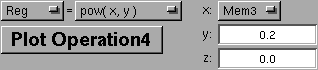
Die beiden Argumente "y" und "z" tragen Sie direkt in die Zahlen-Anzeige ein.
Mit diesem Pop-Up-Menü wählen Sie das Ergebnis-Register bzw. das 1. Argument der Operation4:
Die Funktion bzw. den Vergleich von Operation4 wählen Sie mit diesem Pop-Up-Menü:
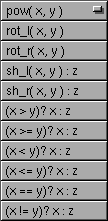
| pow( x, y ) | potenziert Register x hoch Argument y; |
| rot_l( x, y ) | rotiert Register x um den ganzzahligen Anteil von y in Samples Richtung links (d.h. die Samples, die links herausfallen, werden rechts wieder hinein-rotiert); |
| rot_r( x, y ) | wie rot_l nur Richtung rechts; |
| sh_l( x, y ) | schiebt Register x um den ganzzahligen Anteil von y in Samples Richtung links (von rechts wird das Argument z hineingeschoben); |
| sh_r( x, y ) | wie sh_l nur Richtung rechts; |
| ( x > y )? x : z | wenn der Wert von Register x größer als y ist, dann bleibt x = x, sonst wird x ersetzt durch x = z; |
| ( x >= y )? x : z | der Vergleich findet hier mit "x größer oder gleich als y" statt; |
| ( x < y )? x : z | der Vergleich findet hier mit "x kleiner als y" statt; |
| ( x <= y )? x : z | der Vergleich findet hier mit "x kleiner oder gleich als y" statt; |
| ( x == y )? x : z | der Vergleich findet hier mit "x gleich y" statt; |
| ( x != y )? x : z | der Vergleich findet hier mit "x ungleich y" statt; |
Indem Sie den Button "Plot Operation4" anklicken, bewirken Sie wieder die bereits bekannten 3 Dinge:
- Das Ergebnis-Register wird laut Zuweisungs-Vorschrift berechnet.
- Die graphische Darstellung des Ergebnis-Registers wird aktualisiert und neu angezeigt.
- Falls Sie "Reg" als Ergebnisregister eingestellt haben, wird es optional in das MAX-External-Objekt übertragen.
4.4.5 Die Begrenzungen
Die y-Richtung von Register "Reg" ist konstant zwischen -1.0 und +1.0 begrenzt.
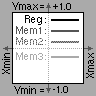
Die Grenzen in x-Richtung können Sie mit diesen 2 mal 4 Buttons setzen oder sie direkt in die beiden Textfelder eintragen.

Die Grenzen in x-Richtung wirken sich eigentlich nur für "Plot Operation1" aus, und zwar dann, wenn die Zuweisungs-Vorschrift auf "Register = x" ( die "y = x"-Gleichung ) lautet.
Die Skalierung der drei Hintergrund-Register "Mem1", "Mem2" und "Mem3" in y-Richtung erfolgt automatisch in Zehner-Potenz-Schritten ( 0.1, 1.0, 10.0, 100.0 usw. ):

Wenn "Reg" in y-Richtung über die Begrenzungswerte von -1.0 bzw. +1.0 hinausgeht oder diese stark unterschreitet, klicken Sie auf "Normalize".

Achtung: "Normalize" ist nicht mehr rückgängig zu machen! Wenn Sie eine Wavetable weiter entwickeln wollen, sollten Sie sie speichern, bevor Sie diesen Befehl geben.
4.5 Manual Editing
In der Betriebsart Manual Editing haben Sie 4 verschiedene Möglichkeiten, Wavetables durch Zeichnen mit der Maus zu erstellen bzw. zu editieren:

- Normales Zeichnen:
Wenn Sie die Maus nur mit gedrückter linker Taste bewegen, können Sie einen beliebigen Polygon-Zug zeichnen. Erst wenn Sie die Maus-Taste losgelassen haben, wird die Wavetable neu gezeichnet und optional in das MAX-External-Objekt übertragen. - Zeichnen + Shift-Taste:
Wenn Sie die Maus mit gedrückter linker Taste bewegen und während der gesamten Zeit auch die Shift-Taste gedrückt halten, zeichnen Sie eine Gerade vom Ausgangspunkt bis zur aktuellen Maus-Position. - Zeichnen + Alternate-Taste:
Wenn Sie die Maus mit gedrückter linker Taste bewegen und während der gesamten Zeit auch die Alternate-Taste gedrückt halten, können Sie einen beliebigen Bereich der Wavetable entlang der x-Achse grau unterlegen. Jene beiden Punkte der Wavetable, die diesen Bereich begrenzen, werden direkt durch eine Gerade verbunden. - Zeichnen + Control-Taste:
Diese Kombination funktioniert analog zu Punkt 3 (Zeichnen + Alternate-Taste). Allerdings werden hier die beiden Punkte der Wavetable, die den grauen Bereich begrenzen, durch eine Polynomkurve dritter Ordnung verbunden. Dadurch werden die beiden Teile der Wavetable, die außerhalb des unterlegten Bereichs liegen, ohne Knick miteinander verbunden.
Die Wavetable wird erst dann neu gezeichnet und optional in das MAX-External-Objekt übertragen, wenn Sie die Maus-Taste losgelassen haben.
Wenn Sie die Kennlinie auf 0.0 setzen wollen, dann klicken Sie auf "Set 0.0".
Möchten Sie die Kennlinie auf eine 45 Grad-Gerade setzen, die als Sägezahn-Funktion bzw. als 1 : 1 Verzerrungs-Kennlinie dienen kann, dann klicken Sie auf "Set y = x".
Die x- und die y-Richtung ist konstant zwischen -1.0 und +1.0 begrenzt.
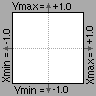
Um die Wavetable in y-Richtung innerhalb der Grenzen von -1.0 und +1.0 zu normieren, klicken Sie auf "Normalize".

Mit dieser Option wird das Zeichnen von negativen Werten verhindert. Wenn Sie den Switch aktivieren, werden alle negativen Wavetable-Werte auf 0.0 gesetzt .
Wenn Sie eine Wavetable aus einer anderen Betriebsart in diesen Modus importieren wollen (Waveshaping, Fourier Synthesis oder Mathematical Calculation), dann klicken Sie auf einen der 3 Buttons:

Diese beiden Textfelder zeigen die aktuelle Mausposition innerhalb des Zeichenfeldes an (-256.....+255):
5. Die Kommunikation zwischen WaveTabShaper und MAX
Wenn Sie eine Wavetable entwickeln wollen, stehen Ihnen im Ordner "MaxPatches" je nach Verwendungsart einer der 6 folgenden Max-Patches zur Verfügung:
| Distortion2.pat | (Verzerrungs-Kennlinien in den Betriebsarten Mathematical Calculation und Manual Editing) |
| Envelope2.pat | (Hüllkurven in den Betriebsarten Mathematical Calculation und Manual Editing) |
| Oscillator2.pat | (stetige Oszillator-Wavetablesin der Betriebsart Fourier Synthesis) |
| Oscillator2_I.pat | (unstetige Oszillator-Wavetables in den Betriebsarten Mathematical Calculation und Manual Editing) |
| WaveShape2.pat | (Verzerrungs-Kennlinien in der Betriebsart Waveshaping mit 2-Punkt-interpolation) |
| WaveShape4.pat | (Verzerrungs-Kennlinien in der Betriebsart Waveshaping mit 4-Punkt-interpolation) |
Alle 6 Patches haben die beiden receive-Objecte: "r maxwave_resp" und "r init_mess" gemeinsam, sowie eines
der 6 Kern-Objekte: "dist2~", "env2~" , "osc2~" , "osc2_I~", "env2~" ,
"wshape2~" und "wshape4~".
Diese Kern-Objekte empfangen die 512 Sample-Werte von WaveTabShaper , und führen ihre jeweilige Funktion aus. Der einzige Nachteil bei
Verwendung dieser Kern-Objekte ist, daß sie relativ viel Prozessor-Leistung verbrauchen (ca. 10 % bei 44100 Hz Samplerate). Die Zeichenfolge "_I" von
"Oscillator2_I.pat" deuten auf eine Unstetigkeitsstelle hin.
Wenn Sie nun geeignete Wavetables entwickelt und gespeichert haben, können Sie mittels der 4 folgenden Patches diese Wavetables anwenden:
| Tab1Distortion.pat | (Verzerrungs-Kennlinien, erzeugt in den Betriebsarten Mathematical Calculation und Manual Editing) |
| Tab1Envelope.pat | (Hüllkurven, erzeugt in den Betriebsarten Mathematical Calculation und Manual Editing) |
| Tab1Oscillator.pat | (stetige und unstetige Oszillator-Wavetables, erzeugt in den Betriebsarten Fourier Synthesis, Mathematical Calculation und Manual Editing) |
| Tab1WaveShape.pat | (Verzerrungs-Kennlinien, erzeugt in der Betriebsart Waveshaping) |
Die 4 Kern-Objekte dieser 4 Patches lauten: "tab1dist~" , "tab1env~" , "tab1osc~" und
"tab1wshape~".
Die Zeichenfolge "tab1" dieser Patches bzw. dieser Kern-Objekte weist darauf hin, daß Sie, bei der Verwendung dieser
Kern-Objekte, für jede Wavetable mittels dem Max-Objekt "tab1~wavetablename.snd" Speicherplatz reservieren
müssen. Die Prozessor-Leistung eines Kern-Objektes beträgt dann ca. 1.5 %. Für diese Patches ist es natürlich nicht mehr notwendig,
daß Sie das Programm WaveTabShaper gestartet haben.
6. Beispiele
Beispiel zu Mathematical Calculation:Berechnung eines symmetrischen Gewichtungs-Fensters (ähnlich wie Hanning-Window ), das sich aus 5 Teilen zusammensetzt:
- 12.5 % 0.0;
- 25% ansteigende Cosinus-Halbwelle von 0.0 auf 1.0;
- 25 % 1.0;
- 25% abfallende Cosinus-Halbwelle von 1.0 auf 0.0;
- 12.5 % 0.0;
Dazu setzen Sie zuerst die Grenzen "x-max" auf "2Pi" bzw. "x-min" auf "-2Pi".
Dann stellen Sie bei der Operation1 "Mem3 = x" ein und klicken auf "Plot Operation1".
Dann stellen Sie bei der Operation2 "Mem2 = sin(x)" und "x: Mem3" ein und klicken auf "Plot Operation2".
Dann stellen Sie bei der Operation1 "Mem3 = const." und "const: 0.5" ein und klicken auf "Plot Operation1".
Dann stellen Sie bei der Operation3 "Mem2 = Mem2 * Mem3" ein und klicken auf "Plot Operation3".
Dann stellen Sie bei der Operation3 "Mem2 = Mem2 + Mem3" ein und klicken auf "Plot Operation3".
Dann stellen Sie bei der Operation4 "Mem2 = sh_r(x,y):z" , "x: Mem2", "y: 64" und "z: 0.0" ein und
klicken auf "Plot Operation4".
Dann stellen Sie bei der Operation4 "Mem2 = sh_l(x,y):z" , "x: Mem2", "y: 256" und "z: 0.0" ein und
klicken auf "Plot Operation4".
Dann stellen Sie bei der Operation4 "Mem1 = sh_l(x,y):z" , "x: Mem2", "y: 128" und "z: 1.0" ein und
klicken auf "Plot Operation4".
Dann stellen Sie bei der Operation4 "Mem2 = sh_r(x,y):z" , "x: Mem2", "y: 384" und "z: 0.0" ein und
klicken auf "Plot Operation4".
Dann stellen Sie bei der Operation4 "Mem2 = rot_l(x,y)" , "x: Mem2" und "y: 320" ein und klicken auf
"Plot Operation4".
Dann stellen Sie bei der Operation4 "Mem1 = rot_r(x,y)" , "x: Mem1" und "y: 320" ein und klicken auf
"Plot Operation4".
Zuletzt stellen Sie bei der Operation3 "Reg = Mem2 + Mem1" ein und klicken auf "Plot Operation3".
7. Theoretische Abhandlung von Waveshaping
Waveshaping ist eine effiziente Form von Oberwellen-Erzeugung eines Signals.Der Oberwellen-Gehalt ist stark abhängig von der Amplitude des Eingangs-Signals.
In dieser Betrachtung nehmen wir ein Cosinusförmiges Eingangs-Signal mit der Amplitude von 1.0 an.
Die Transfer-Funktion (Ausgangs-Signal / Eingangs-Signal) ist im allgemeinen eine nichtlineare Verzerrungs-Kennlinie, die als Polynom des Eingangs-Wertes dargestellt wird.
x = cos(wt)
1 = cos(0)
Wie Sie sehen können, ist dieses Koeffizienten-Schema dem Pascal'schen Dreieck sehr ähnlich.
Mittels einer Korrektur in der ersten Zeile (von 1 auf 0.5) wurde die erste Spalte (div) der Folge 2(n-1) angepaßt. Die zweite Spalte zeigt nun den doppelten
Wert vom Koeffizienten der 0. Harmonischen.
Angenommen, man strebt an, nur die reine 5. Harmonische einer Verrzerrung zu gewinnen, benötigt man primär die x5-Potenz-Funktion.
Diese erzeugt aber auch eine 3. und eine 1. Harmonische.
x = cos(wt)
x = h1
y = a1*x + a3*x3 + a5*x5 = h5
h5: a5/16 = 1
h3: a3/4 + a5*5/16 = 0
h1: a1/1 + a3*3/4 + a5*10/16 = 0
Das heißt: mit dem Polynom y = 5*x - 20*x3 + 16*x5 erzeugt man aus einem Cosinus-Signal mit der Amplitude 1.0 und der Frequenz f ein
Cosinus-Signal mit der Frequenz 5*f.
Zur allgemeinen Lösung dieser Gleichungen n-ter Ordnung verwendet man die Tschebyscheff-Polynome.
T0(x) = 1;
Die Koeffizienten der Tschebyscheff-Polynome sind identisch mit den Koeffizienten der Potenz-Reihe, die zur n-fachen harmonischen Verzerrung eines Cosinus-Signals dient.
Wenn Sie nun eine beliebige Oberwellen-Verteilung eines Signals wünschen, müssen Sie nur mehr die einzelnen Koeffizienten der Tschebyscheff-Polynome
bezüglich ihrer Potenz-Ordnug addieren, und erhalten damit das gesamte Waveshaping-Polynom. Dieses Polynom wird dann im Argument-Bereich von x zwischen
-1.0 bis +1.0 in n Schritten diskutiert.
BECAUSE THE PROGRAM IS LICENSED FREE OF CHARGE, THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE
LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM "AS IS"
WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE OF THE
PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MAY
MODIFY AND/OR REDISTRIBUTE THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL
OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA
BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER
PROGRAMS), EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.
x = cos(wt)
x2 = (1 + cos(2wt)) / 2
x3 = (3*cos(wt) + cos(3wt)) / 4
x4 = (3 + 4*cos(2wt) + cos(4wt)) / 8
x5 = (10*cos(wt) + 5*cos(3wt) + cos(5wt)) / 16
.............
| div | h0 h1 h2 h3 h4 h5 h6
----------------------------------------------------------------------------------
x0 | 1 | 1
x1 | 1 | 0 1
x2 | 2 | 1 0 1
x3 | 4 | 0 3 0 1
x4 | 8 | 3 0 4 0 1
x5 | 16 | 0 10 0 5 0 1
x6 | 32 | 10 0 15 0 6 0 1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Nun stellt dieses Schema das halbe Pascal'schen Dreieck dar.
| div | h0 h1 h2 h3 h4 h5 h6
----------------------------------------------------------------------------------
x0 | 0,5 | 1
x1 | 1 | 0 1
x2 | 2 | 2 0 1
x3 | 4 | 0 3 0 1
x4 | 8 | 6 0 4 0 1
x5 | 16 | 0 10 0 5 0 1
x6 | 32 | 20 0 15 0 6 0 1
Die störenden Harmonischen kann man verhindern, indem man die x1 - und die x3- Potenz-Funktion geeignet multipliziert und
zur x5 -Potenz-Funktion addiert. Das entspricht der Lösung eines Gleichungs-Systems 5. Ordnung.
x3 = (3*cos(wt) + cos(3wt)) / 4
x5 = (10*cos(wt) + 5*cos(3wt) + cos(5wt)) / 16
x3 = (3*h1 + h3) / 4
x5 = (10*h1 + 5*h3 + h5) / 16
a5 = 16;
a1 = 5;
Diese lauten:
T1(x) = x;
T2(x) = 2*x2 - 1;
T3(x) = 4*x3 - 3*x;
T4(x) = 8*x4 - 8*x2 + 1;
T5(x) = 16*x5 - 20*x3 + 5*x;
T6(x) = 32*x6 - 48*x4 + 18*x2 - 1;
........
Tn(x) = 2*x*Tn-1(x) - Tn-2(x);
Literatur-Verweise:
"COMPUTER MUSIC" von Charles Dodge und Thomas A. Jerse, 1985 Schirmer Books; Seite 128 bis 146.
8. Anhang
NO WARRANTY

