Beiträge zur Elektronischen Musik 5
3. "Real Time Composition Library"
Eine Softwarebibliothek zum Design von Strukturgeneratoren
3.1. Komponieren mit Computerunterstützung
Es existieren im Wesentlichen zwei grundsätzliche Methoden, den Computer als Werkzeug im Kompositionsprozeß einzusetzen. Die am häufigsten praktizierte verwendet den Rechner als komfortable Schreibmaschine, mit der musikalische Einfälle aufgezeichnet und manipuliert werden können. Als Ergebnis liefern sie entweder eine elektronisch erstellte Partitur, die dann von Musikern gespielt wird (Notationsprogramm), oder eine Folge von Steueranweisungen, mit der elektronische Musikinstrumente angesteuert werden (Sequenzer).
Die andere Methode, der ich mich ausschließlich widme, sieht den Computer als experimentelle Werkbank, um kompositorische Ideen zu entwickeln und erproben. Mit Hilfe einer geeigneten Programmiersprache lassen sich kompositorische Algorithmen formulieren und umsetzen. In der Interaktion mit dem Computer kann der Komponist die Tragweite seiner kompositorischen Absichten erkennen, ohne jedoch das Zepter aus der Hand zu geben. Ist er mit den Resultaten nicht einverstanden, kann er das Programm solange modifizieren, bis Intention und Ergebnis zur Deckung gebracht sind. Dabei umschließt das künstlerische Subjekt als erste und letzte Instanz wie eine Klammer den gesamten Kompositionsprozeß: es entwirft ein Modell, analysiert dessen Output und gewinnt dadurch neue Erkenntnisse, die dazu führen mögen, die Ansätze neu zu formulieren oder das Modell zu modifizieren. So kann der Computer zu einer — selbstgeschaffenen — Kontrollinstanz werden, zum unbestechlichen Spiegel der eigenen Vorstellung.
3.2. MAX
Als ich 1992 ans IRCAM kam, um dort an einem Kompositionsauftrag38 für Ensemble und die “IRCAM Musical Workstation” (ISPW)39 zu arbeiten, lernte ich auch die Programmiersprache MAX in kennen, welche die graphische Benutzeroberfläche der ISPW darstellt.
Die Entwicklung von MAX40 wurde 1986 am IRCAM begonnen, als man das Paradigma eines Analogstudios41, dessen einzelnen Komponenten durch Kabelverbindungen zu komplexeren “Patches” verschaltet werden können, auf eine graphische Programmierumgebung übertrug. Die grundlegende Absicht war es, ein Echtzeitsystem zu entwickeln, das vor allem im Live-Einsatz Verwendung finden sollte. Aus einem kleinen Vorrat von System-”Primitives” (graphischen Objekten mit Ein– und Ausgängen) lassen sich durch Verbindungen mit sog. “patch chords” höherstrukturierte Objekte erzeugen. Ein solcher “Patch”, dessen interne Komplexität hinter einer “object box” verborgen werden kann, kann nun als eigenes Objekt angesprochen werden. Dadurch lassen sich komplizierte Strukturen aus einigen hochspezialisierten Objekten (Unterprogrammen vergleichbar) erzeugen, die wiederum aus untergeordneten Objekten bestehen usw.
Solche Objekte, die Erweiterungen des Sprachschatzes darstellen, können nun in verschiedenen Kontexten verwendet werden, ohne daß man sich jeweils die genaue Kenntnis ihrer internen Organisation vor Augen führen muß. Sie fungieren als “black boxes”, deren Verhalten man zwar genau kennen soll, ohne aber über die programmtechnischen Details Bescheid wissen zu müssen.
3.3. RTC-lib
MAX dient in erster Linie zur Manipulation von MIDI-Daten42, also Steuerinformationen für elektronische Musikinstrumente. Was bislang aber fehlte, war eine Bibliothek mit speziellen Funktionen für “Computer Aided Composition”. Diese Lücke füllt nun die seit 1992 entwickelte “Real Time Composition Library for MAX”. Mit dieser Bibliothek von Softwaremodulen lassen sich Kompositionsalgorithmen auf einer hohen Abstraktionsebene formulieren, ohne daß der Benutzer sich mit untergeordneter Systemprogrammierung abplagen muß.
Als Beispiel sei etwa das Objekt scale angeführt, das Werte aus einem bestimmten Eingangsintervall in ein definierbares Ausgangsintervall umrechnet (“skaliert”):
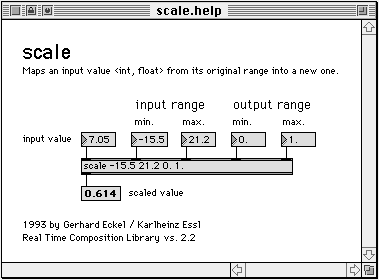
Abb. 3: Help-File der Funktion scale
Im Inneren dieser Funktion verbirgt sich eine aus MAX-Primitives konstruierte Programmstruktur, die – einmal implementiert – in den verschiedensten MAX-Patches verwendet werden kann (“re-usability”), ohne daß man sich jedesmal den Berechnungsalgorithmus vergegenwärtigen muß. Ist die Funktion einmal ausgetestet und ihr Verhalten bekannt, kann sie wie eine Systemfunktion benutzt werden.
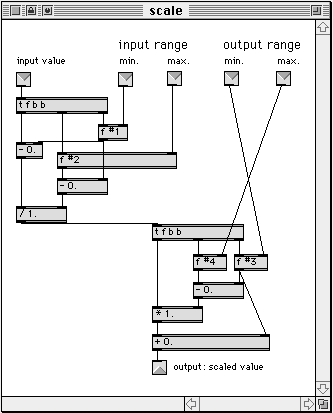
Abb. 4: Das verborgene Innenleben von scale
Das Prinzip, durch Programmierung von Softwaremodulen den Grundwortschatz einer Computersprache zu erweitern, habe ich bereits in meinem auf xLOGO basierendem COMPOSE-Environment (1988 ff.) angewandt. Dieses System verwende ich in erster Linie zur Generierung von “score listings”, deren symbolisch-numerische Erscheinung zunächst in musikalische Notation übersetzt werden müssen, um zu klanglichen Ergebnissen zu gelangen.43
In MAX hingegen bietet sich die Möglichkeit, alle Operationen in Echtzeit durchzuführen. Damit läßt sich nunmehr ein lang gehegter Traum verwirklichen: die Schaffung einer experimentellen Werkbank zur Entwicklung und Erprobung kompositorischer Strategien, deren Ergebnisse sofort hörbar gemacht werden können. Diese Unmittelbarkeit bringt naturgemäß enorme Vorteile für den Entwicklungsprozeß einer Komposition, da augenblicklich sinnliche Erfahrungen gesammelt werden können. Dadurch läßt sich eine zunächst nur grob skizzierte kompositorische Idee schrittweise verfeinern, bis Intention und Resultat – in einem Rückkopplungsprozeß zwischen Komponist und Computer – zur Deckung gebracht werden (“rapid prototyping”).
Der unmittelbare Respons eröffnet aber auch die Möglichkeit, Musikautomaten zu erfinden, die Musik in einem immerwährender Prozeß in Echtzeit generieren. 44Diesen Ansatz nannte ich einmal scherzhaft “Realtime Composition”, wohl um die Paradoxie dieses Wortpaares wissend. Mittlerweile hat sich dieser Begriff aber eingebürgert, und eine ganze Bibliothek von Softwaremodulen – eben die “Real Time Composition Library” (RTC-lib) trägt diesen Namen.
Die “Real Time Composition Library” stellt ein work-in-progress dar und erscheint mittlerweile in der Version 2.2. Die Arbeit daran wurde 1992 begonnen, als ich gemeinsam mit Gerhard Eckel (IRCAM) Überlegungen anstellte, welche grundlegenden MAX-Funktionen für musikalische Komposition notwendig wären. Ihm verdanke ich auch die Entwicklung einiger toolbox-Objekte und die Einführung in einen strukturierten und objekt-orientierten Programmierstil.
Die Version 1.0 wurde ursprünglich vom IRCAM im Rahmen der “IRCAM Usergroup” vertrieben. Die mittlerweile als Version 2.2. erscheinende RTC-lib (verbessert und stark erweitert, mit Hypertext-artiger Online-Hilfe, Tutorial und Anwendungsbeispielen) ist nunmehr Public Domain-Software und kann im Internet von verschieden ftp-servern bezogen werden.45 Neben Gerhard Eckel haben auch andere Personen Beiträge zur RTC-lib geleistet, denen an dieser Stelle gedankt sein soll: allen voran Peter Elsea (University of California, Santa Barbara), der manche bereits bestehende RTC-Objekte als Externals in C implementierte und die Erlaubnis gab, einige seiner Listenobjekte in die RTC-lib zu integrieren; weiters Orm Finnendahl (Berlin), James McCartney (University of Texas), David Zicarelli (IRCAM / Paris), Gary Lee Nelson (Oberlin College) und Charles Baker.
Die RTC-lib ist in ständiger Veränderung begriffen und reflektiert den momentanen Stand meiner kompositionstheoretischen Auseinandersetzung. Ihre Charakteristika seien hier in Kürze zusammengefaßt:
- ein offenes und erweiterbares, objekt-orientiertes “Realtime Programming
Environment” anstelle eines starren, geschlossenen Computerprogrammes,
- modular aufgebaut,
- die RTC-Objekte können in verschiedensten Kontexten verwendet werden
(“re-usability of code”),
- Komplexität kann durch Kapselung (encapsulation) verborgen werden.
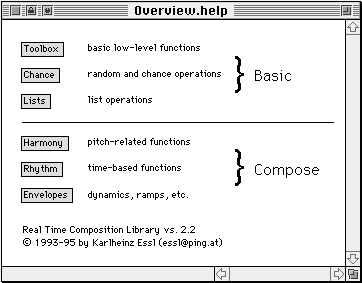
Abb. 5: Aufbau der RTC-lib
Die “Real Time Composition Library” besteht aus 145 Objekten, die sich in zwei grundsätzliche Kategorien unterteilen lassen: Basic-Objekte für die Bewältigung programmtechnischer Probleme und Compose-Objekte für spezielle kompositorische Fragestellungen. Diese Grundkategorien lassen sich nun weiter klassifizieren.
- BASIC
- Toolbox: grundlegende low-level Funktionen
- Chance: Zufallsoperationen
- Lists: Listenoperationen46
- COMPOSE
- Harmony: tonhöhenbezogene Funktionen
- Rhythm: rhythmus- und zeitbezogene Funktionen
- Envelopes: Hüllkurven und zeitvariante Funktionen ("ramps")
Die Library erlaubt es dem Anwender, sich mehr auf die kompositorischen Fragestellungen zu konzentrieren, da die Entwicklung von Programmstrukturen auf einem sehr hohen Level erfolgt. Dafür werden dem Benutzer eine Vielzahl von Werkzeugen zur Verfügung gestellt. Davon möchte ich im Folgenden nun einige Kategorien exemplarisch herausgreifen – und zwar Zufallsoperationen, Rhythmus- und Harmoniegeneratoren.
3.3.1. Zufallsoperationen
Die nachfolgende Übersicht zeigt alle Zufallsoperationen, die bislang in der RTC-lib verfügbar sind:
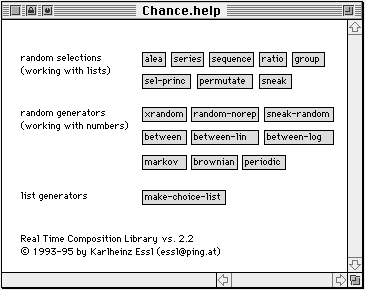
Abb. 6: Zufallsoperationen in der RTC-lib
Es lassen sich zwei grundsätzliche Kategorien unterscheiden: a) Zufallsgeneratoren und b) Selektionsmechanismen.
ad a) Zufallsgeneratoren generieren Zufallszahlen innerhalb eines gegebenen Wertebereichs. Das Verhalten kann gelegentlich durch Zusatzparameter beeinflußt werden. Um die verschiedenen Generatoren miteinander zu vergleichen, wurden von jedem Algorithmus 40 Zufallszahlen zwischen 0 und 5 berechnet, und die Ergebnisse in Kästchen dargestellt.
Der einfachste Zufallsgenerator – between – liefert jede beliebige Zahl aus einem angegeben Intervall und verkörpert so den “blinden Zufall”. Betrachten wir die Verteilung der Zahlen über die Zeit, so erkennen wir keinerlei Regelmäßigkeiten oder Strukturen. Sicher ist nur, daß im statistischen Mittel alle Werte gleich häufig auftreten.

Abb. 7a: between
Eine etwas “intelligentere” Variante stellt xrandom dar. Aufgrund eines implementierten Wiederholungsverbotes darf eine Zahl erst dann wieder ausgegeben werden, wenn alle anderen bereits vorgekommen sind (worin sich noch altes serielles Denken widerspiegelt). Die Wiederholung gleicher Werte kann nur an den “Nahtstellen” erfolgen (in untenstehender Graphik eingekreist) – wenn also die letzte Zahl eines Durchlaufs und die erste des nächsten zufälligerweise gleich sind.

Abb. 7b: xrandom
Der in der serielle Gruppentheorie durch Koenig eingeführte Begriff der “Periodizität”47 hat im Zufallsgenerator periodic seinen Niederschlag gefunden. Hier wird das in xrandom geltende Wiederholungsverbot durch ein Wiederholungsgebot ersetzt. Ein Periodizitätsfaktor (zwischen 0 und 1) bestimmt, wie oft ein zufällig gewählter Wert wiederholt werden kann, ehe ein neuer berechnet wird. Die durchschnittliche Gruppengröße steigt also mit dem Periodizitätfaktor; ist dieser 1, wird immerfort der gleiche Wert repetiert, ist er hingegen 0, herrscht wiederum das Wiederholungsverbot.

Abb. 7c: periodic
In den drei zuvor beobachteten Zufallsgeneratoren spielte für die Generierung der nächsten Zahl die vorhergehende keine Rolle. Anders in brownian, wo die Idee der Brown’schen Molekularbewegung (“random walk”) umgesetzt wurde. Ein zusätzlicher Parameter (der sog. “brown factor”, auch als Freiheitsgrad bezeichnet) bestimmt hier, wie groß das Intervall zwischen zwei benachbarten Zufallszahlen sein darf. Ein Faktor von 1 bedeutet, das Intervall zweier benachbarter Zahlen beliebig sein kann, was exakt dem Verhalten des “blinden” Zufallsgenerators between entspricht. Ein Faktor von 0 wiederum würde dazu führen, daß immer nur eine einzige Zahl ausgegeben werden kann. Bei einem entsprechend gewählten “brown factor” (0.27 in untenstehender Graphik) kann das Verhalten so eingestellt werden, daß immer nur eng benachbarte Zahlenwerte generiert werden können.

Abb. 7d: brownian
ad b) Selektionsmechanismen hingegen wählen Elemente aus einem gegebenem Repertoire (“supply”) aus, arbeiten deshalb auf einer höheren Abstraktionsebene: Das Augenmerk richtet sich hier auf eine bestimmte Materialkonstellation (eine Liste), die entweder frei definiert werden kann, oder (funktionell gedacht) wiederum mit Hilfe einer listengenerierenden Funktion erzeugt werden kann.
Die von Koenig in Projekt 1 und Projekt 2 definierten Selektionsmechanismen alea, series, sequence, ratio und group wurden für die RTC-lib neu in MAX implementiert. So liefert beispielsweise sequence das jeweils nächste Element der Repertoireliste,
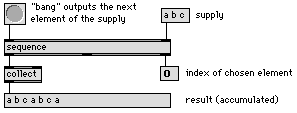
Abb. 8: sequence
während alea jedes beliebige Element ausgeben kann.
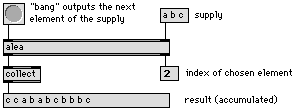
Abb. 9: alea
3.3.2. Rhythmus
Bevor ich mich nun den Rhythmusgeneratoren widme, möchte ich zunächst einige Anmerkungen zur Nomenklatur machen:
Der Abstand zwischen zwei rhythmischen Impulsen wird Einsatzabstand (“entry delay”) genannt und ist eine relative Zeitangabe. Die absolute Zeitbestimmung wäre nun der Einsatzpunkt (“entry point”), den man durch sukzessives Aufaddieren der Einsatzabstände erhält. Die Dauer wiederum bezeichnet, wie lange ein Ereignis zu einem gegebenen Einsatzpunkt dauert. Als zusätzliche Bestimmungsgröße des Rhythmus ließe sich auch die Akkordgröße (vertikale Dichte) bestimmen, die angibt, wie viele Ereignisse (“events”) an einem Einsatzpunkt zugleich stattfinden.
Folgende “score list” eines kurzen rhythmischen Ablaufs:
Einsatzabstand Akkordgröße Dauer
0.0 3 0.8
1.2 1 3.0
0.8 2 0.1
1.5 1 1.7
0.2 4 0.7
würde folgendes – graphisch interpretiertes – Ergebnis liefern:
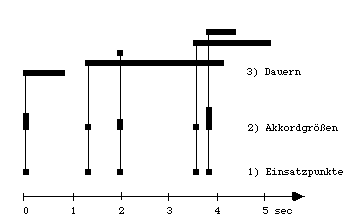
Abb. 10: Rhythmus-Parameter
Die drei den Rhythmus beschreibenden Parameter (Einsatzabstand, Akkordgröße und Dauer) wurden in dieser graphischen Repräsentation voneinander isoliert aufgezeichnet, fallen aber in der musikalischen Realität natürlich zusammen und bilden ein Ganzes.
Rhythmusgeneratoren
In der RTC-lib gibt es eine Reihe von Rhythmusgeneratoren mit unterschiedlichen Eigenschaften. Hier wurden verschiedene kompositionstheoretischen Ansätze als Modelle implementiert, deren Parameter innerhalb festgelegter Grenzen verändert werden können.
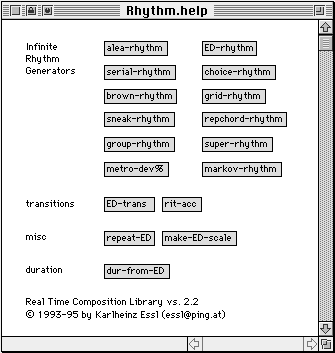
Abb. 11: Rhythmusobjekte der RTC-lib
Aus den oben angeführten Rhythmusgeneratoren möchte ich nun einen einzelnen herausgreifen: repchord-rhythm.
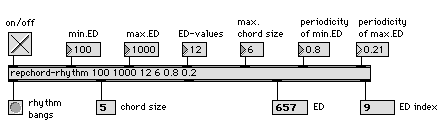
Abb. 12: repchord-rhythm
Es handelt sich dabei um einen “unendlichen” Rhythmusgenerator, der – einmal eingeschaltet – fortwährend eine charakteristische rhythmische Faktur erzeugt. Diese ist abhängig von den 6 Parametern:
- min.ED ("minimum entry delay"): kleinster Einsatzabstand (ms)48
- max.ED ("maximum entry delay"): größter Einsatzabstand (ms)
- nr.of.ED ("number of entry delays"): Anzahl der Einsatzabstände
- max.chordsize: maximale Akkordgröße
- periodicity of min.ED: Periodizität des kleinsten Einsatzabstandes
- periodicity of max.ED: Periodizität des größten Einsatzabstandes
Zunächst wird als rhythmisches Ausgangsmaterial eine geometrische Reihe aus min.ED und max.ED mit nr.of.ED Gliedern gebildet49. Aus diesem Vorrat werden mit Hilfe des Selektionsmechanismus alea zufällige Einsatzabstände ausgewählt.
Die Entscheidung, wie oft nun der gewählte rhythmische Wert wiederholt wird, ist von den zwei Periodizitätsfaktoren abhängig. In der Regel wird man den Periodizitätsgrad der min.ED relativ hoch ansetzen, während der von max.ED geringer zu veranschlagen ist. Das würde bedeuten, daß schnellere rhythmische Werte größere Ketten bilden (also ein periodischeres Verhalten an den Tag legen), während lange Notenwerte weniger oft repetiert werden.
Zuletzt wird in Abhängigkeit zum gewählten Einsatzabstand noch die Akkordgröße des rhythmischen Impulses bestimmt. Dabei herrscht folgende Relation: große Einsatzabstände können Akkordgrößen bis zur angegeben max.chordsize aufweisen, während der kleinste rhythmische Wert nur Akkordgrößen von 1 (= Einstimmigkeit) zugewiesen bekommt.
Aus diesem Modell lassen sich durch Veränderung der Parameter unterschiedlichste Varianten bilden, die für sich wiederum unendliche viele rhythmische Gestalten erzeugen können.
3.3.3. Harmonik
Ein rhythmischer Ablauf, wie ihn ein Rhythmusgenerator der RTC-lib generieren kann, bedarf zu seiner Konkretisierung – Versinnlichung! – eines weiteren Parameters: den des Klanges. Erst im Klang selbst manifestiert sich das Rhythmische als sinnlich wahrnehmbare Gestalt.
Klang läßt sich nun ebenfalls parametrisch beschreiben. Ein wichtiger Aspekt ist seine Frequenz, spezifischer: seine Tonhöhe. Tonhöhe tritt nur in den seltensten Fällen als isolierte Größe auf – wir hören sie immer in Relation zueinander, und konstruieren uns bei Hören harmonische Bezüge. »Harmonik« bezieht sich nun eben nicht auf das punktuelle Ereignis, sondern immer auf den Kontext – also die Beziehungen zwischen den Tönen bzw. Klängen.
Die RTC-lib beinhaltet nun eine ganze Reihe von Funktionen, um harmonische Abläufe zu gestalten.
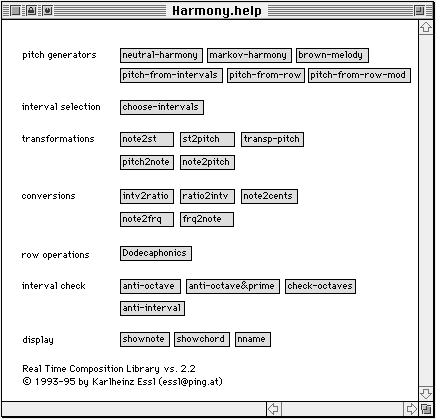
Abb. 13: Harmonie-Objekte der RTC-lib
An dieser Stelle noch ein Exkurs zur Nomenklatur:
- pitch (class): "abstrakte" Tonqualität ohne
Registerangabe, z.B. c, f#
- note: "konkrete" Tonhöhe mit Registerangabe, z.B. c1,
F#
- register: Oktavlage, z.B. 5 = eingestrichene Oktave
- interval: Abstand zwischen zwei "notes", gemessen in
Halbtonschritten, z.B.:
- -1 = absteigende kleine Sekunde
- 19 = aufsteigende Duodezime
- 0.5 = ein Viertelton aufwärts
Zur Veranschaulichung möchte ich nun drei verschiedene Prämissen zur Generierung harmonischer Strukturen vorstellen: ausgehend a) von Tonhöhen (“notes”), b) von Tonqualitäten (“pitch classes”), oder c) von Intervallen. Dies werde ich im Folgenden an Hand von drei verschiedenen Harmoniegeneratoren erläutern, von denen allerdings nur der erste in der RTC-lib aufscheint. Die anderen wurden ausschließlich für diese Publikation und vor allem in Hinblick auf Anschaulichkeit konstruiert.
ad a) Tonhöhenbasierte Harmoniegeneratoren
Nehmen wir nochmals das Modell der “Brown’schen Molekularbewegung”, das wir zuvor im Zusammenhang mit den Zufallsgeneratoren diskutiert haben. Dieses Prinzip läßt sich nun auf die Generierung von Tonhöhen übertragen. Als Wertebereich nehmen wir z.B. den Ambitus eines Klavieres, dessen 88 Tasten den MIDI-Notennummern 21 bis 108 entsprechen. Mit Hilfe des “brown factors” läßt sich nun regulieren, wie groß das Intervall zwischen zwei generierten Tönen maximal sein darf.
Da dieser Ansatz nicht harmonisch (also kontextbezogen) konzipiert ist, treten eine Reihe von möglicherweise unerwünschten Nebeneffekten auf wie etwa “unmotivierte” Tonwiederholungen oder Oktaven. Diese lassen sich nun herausfiltern, wie es im RTC-Objekt brown-melody der Fall ist:
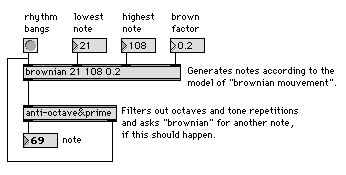
Abb. 14: brown-melody
Dieses einfache Mittel der Filterung verleiht dem, auf einem “dummen” Algorithmus basierenden Tonhöhengenerator, mit einem Male Charakter und Ausgewogenheit.
ad b) Tonqualitätenbasierte Harmoniegeneratoren
Gehen wir nun von einer vorgegebenen Skala von Tonqualitäten aus, die als Material für eine harmonische Struktur dient. Diese Skala wird in einer Liste zusammengefaßt. Aus diesem “supply” werden nun mit Hilfe eines Selektionsmechanismus’ die “pitch class” ausgewählt.
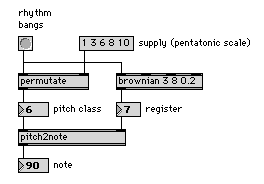
Abb. 15: scale-harmony
Der hier verwendete Selektionsmechanismus heißt permutate: die im “supply” enthaltenen Werte werden zufällig ausgelesen, wobei jedoch direkte Wiederholungen des selben Elements ausgeschlossen sind. Das Resultat ist zunächst aber noch eine nackte Tonqualität (“pitch class”) ohne konkrete Positionierung im Tonraum. Dies besorgt nun die Registerangabe, die wieder mittels brownian ermittelt wird. Das Objekt pitch2note faßt pitch classes und “register” zusammen und berechnet daraus die Tonhöhe (“note”).
Den “supply” haben wir in diesem Fall explizit als pentatonische Skala übergeben. Stattdessen ließe sich aber auch eine Funktion erfinden, die verschiedenste Skalen algorithmisch konstruiert und zur Verfügung stellt. Man könnte noch einen Schritt weitergehen und ein weiteres Objekt gestalten, das eine gegebene Tonskala (also den “supply”) sukzessive verändert, indem es etwa immer ein Element der Liste entweder zufügt oder löscht.50
ad c) Intervallbasierte Harmoniegeneratoren
Schreiten wir zuletzt zu dem abstraktesten, gleichwohl aber reizvollsten Möglichkeit, der Harmonieerzeugung mit Hilfe von Intervallen.
Wir beginnen wieder mit einem gegebenen Material, einer Liste von Intervallen. Diese wird nun aber in diesem Beispiel nicht mehr händisch eingegeben, sondern von dem RTC-Objekt choose-intervals bestimmt.51 Dieses “supply” wird nun mittels sequence der Reihe nach ausgelesen. Ist man am Ende der Liste angelangt, wird wieder von vorne begonnen (“looping”).
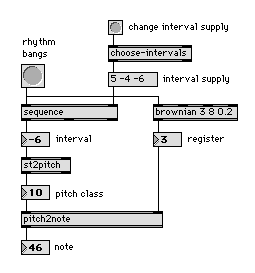
Abb. 16: intervalic-harmony
Auf diese Weise erhält man zunächst Intervalle: hier eine sich zyklisch wiederholende Folge von aufsteigender Quart (= 5), absteigender großer Terz (= -4) und absteigendem Tritonus (= -6). Diese Intervalle werden nun in st2pitch sukzessive aufaddiert und mittels der Operation “modulo 12” die “pitch class” bestimmt. Zur Tonhöhe gelangt man schließlich – wie in obigem Beispiel – wieder durch pitch2note, wo “pitch class” und “register” zusammengefaßt werden.
Wir sehen in diesem Beispiel deutlich die schrittweise “Zubereitung” der harmonischen Gestalt: vom Intervall zur “pitch class” zur Tonhöhe.
3.4. Konstruktion von Strukturgeneratoren
Nachdem wir nun verschieden Teilbereiche der RTC-lib kennengelernt haben, möchte ich nun zeigen, wie damit Strukturgeneratoren konstruiert werden können.
Die im Folgenden wiedergegebene Graphik zeigt das Meta-Modell eines Strukturgenerators zur Generierung von Klaviermusik. Dieses (Meta-Modell) besteht aus vier Patches (mit p gekennzeichnete Objektkästchen, die die konkreten Algorithmen einer musikalischen Struktur beinhalten und nicht einer Softwarebibliothek entnommen sind.
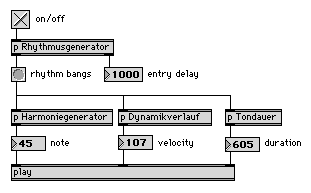
Abb. 17: Flußdiagramm eines Meta-Modells für Strukturgeneratoren
zur Generierung von Klaviermusik
Ein Rhythmusgenerator erzeugt einen bestimmten Rhythmus, indem er rhythmische Impulse (“rhythm bangs”) aussendet. Diese werden an drei weitere Generatoren für Tonhöhe, Tonstärke und Tondauer geschickt und veranlassen diese Objekte, aufgrund ihres implementierten Algorithmus bei jedem Impuls einen entsprechenden Wert zu berechnen. Tonhöhe (“note”), Tonstärke (“velocity”) und Tondauer (“duration”) werden vom Objekt play zusammengefaßt und als MIDI-Informationen an ein angeschlossenes MIDI-Instrument gesendet und dort gespielt.
Wichtig erscheint mir die Feststellung, daß es sich bei dem obigen Beispiel um ein Meta-Modell handelt, das – bei Verwendung verschiedener Rhythmus-, Harmonie-, Hüllkurven- und Dauerngeneratoren – die Konstruktion völlig unterschiedlicher Strukturgeneratoren erlaubt. Die prinzipielle Organisation des Meta-Modells bleibt davon unangetastet: Der primäre Impulsgeber ist immer der Rhythmus, der, mit Tonhöhe, Dynamik und Dauer versehen wird und dadurch erst als musikalische Größe (“Ton”) in Erscheinung tritt. Dies sind auch genau die Parameter, die das Klavierspiel beschreiben: nämlich welche Taste (“note”) zu welchem Zeitpunkt (“entry point”) wie stark angeschlagen (“velocity”) und wie lang gehalten wird (“Dauer”).
Das klingt für’s erste recht nüchtern und gibt Anlaß zur Befürchtung, daß damit nur sehr hölzerne und mechanisch klingende musikalische Abläufe zu gestalten sind. Daß dem nicht so sein muß, soll im letzten Kapitel an Hand der Lexikon-Sonate demonstriert werden.
------------------------------------------------------------
38 Entsagung (1991-93) für Flöte, Baßklarinette, präpariertes Klavier, Schlagzeug und 4-kanaliges interaktives Klang-Environment (TONOS Musikverlags GmbH, Darmstadt).
39 Die ISPW basiert auf einem NeXT-Computer mit spezieller DSP-Hardware und erlaubt die Synthese und Manipulation von Klängen in Echtzeit.
40 Bei MAX (ursprünglich "Patcher" genannt) handelt es sich um eine objekt-orientierte Entwicklungsumgebung für Echtzeitapplikationen. Sie wurde von 1987 von Miller Puckette entworfen und später von David Zicarelli weiterentwickelt. Die Software existiert in zwei unterschiedlichen Varianten: in einer mit Klangverarbeitungs-Funktionen angereicherten Fassung dient sie als Benutzeroberfläche der ISPW, während die von OPCODE Ltd. vertriebene stark erweiterte Machintosh-Version in erster Linie für die Generierung und Manipulation von MIDI-Daten Verwendung findet.
41 Im Analogstudio ließ sich die Idee der Programmierbarkeit von Musik, wie sie die serielle Kompositionstheorie als Möglichkeit anvisiert hatte, erstmals realisieren. Die einzelnen Komponenten (Oszillatoren, Filter, Funktions- und Hüllkurvengeneratoren etc.) werden mittels Steuerspannungen kontrolliert ("voltage control"), können aber wiederum auch selbst Steuerspannungen erzeugen. Diese Ambivalenz ermöglicht die Konstruktion kybernetischer Maschinen, die sich selbst kontrollieren und dabei Klangstrukturen erzeugen (wie etwa in Gottfried Michael Koenigs zwischen 1967 und 1969 entstandene Werkreihe der Funktionen). Eines der wichtigsten Studios dieser Art wurde unter der Leitung von Koenig am "Instituut voor Sonologie" in Utrecht aufgebaut. Der allseits bekannte Moog-Synthesizer stellt die kompakte und bühnentaugliche Version eines Analogstudios dar, wenngleich er mehr zur Erzeugung von "sounds" verwendet wurde als zur Generierung musikalischer Strukturen.
42 MIDI (Musical Instruments Digital Interface) – ein 1983 von verschiedenen Synthesizerherstellern entwickeltes standardisiertes Datenformat zur Steuerung elektronischer Musikinstrumente.
43 cf. Karlheinz Essl, Computer Aided Composition; in: Distel, Nr. 46/47 "Mensch Maschine" (Bozen 1991).
44 Als Beispiel dafür werde ich im Kapitel 4 die Lexikon-Sonate (1992 ff.) – eine unendliche und interaktive Realtime-Komposition für computergesteuertes Klavier – diskutieren.
45 Nähere Informationen finden sich im Anhang des vorliegenden Textes.
46 Um bestimmte Funktionen – zum Beispiel zufallsbasierte Selektionsmechanismen – zu implementieren, war es notwendig, MAX um Listenoperationen zu erweitern. Diese waren ursprünglich nur in rudimentärster Ausprägung im Sprachkonzept von MAX enthalten. Index-Operationen an Reihen (wie wir sie im Kapitel über serielle Theorie diskutiert hatten) lassen sich aber ohne das Konzepte der Liste (oder des "arrays", wie es in prozeduralen Computersprachen heißt) nicht realisieren. Deshalb konnte die Entwicklung der RTC-lib erst in großem Umfang gestartet werden, nachdem auf meine Anregung hin MAX um bestimmte Listenoperationen erweitert wurde. Hier bin ich vor allem Serge Lemouton (IRCAM) zu größtem Dank verpflichtet, der mit der Implementierung eines in C geschriebenen "externals" namens nth (das das n-te Element aus einer Liste ausliest) den Grundstein für viele von mir entwickelten Listenoperationen gelegt hat.
47 Siehe Kapitel 1.6 ("Reihenmanipulationen").
48 Rhythmische Werte werden in der RTC-lib nie in metrischen Einheiten (z.B. Viertel, Achtel etc.) angegeben, sondern immer als absolute Zeitangaben in Millisekunden (ms). Da wir uns hier in einem Bereich außerhalb der traditionellen Notenschrift befinden, können wir uns frei im Feld der Zahlen bewegen, ohne auf metrische Einschränkungen Rücksicht nehmen zu müssen.
49 Siehe den Abschnitt über Zeitreihen im Kapitel 1.8.
50 Ein solches Objekt namens scale-changer existiert bereits in der Version 2.3 der RTC-lib, die sich momentan (Januar 1996) noch im Enwicklungsstadium befindet.
51 Es würde den Rahmen dieser Arbeit übersteigen, wollte ich hier die genaue Funktionsweise von choose-intervals erläutern. Ich beschränke mich, die Eigenschaft dieses Objekts zu beschreiben (und zitiere dabei aus der Online-Dokumentation der RTC-lib): "Chooses a supply of up to five different intervals. This set fullfills certain requirements: the sum of the chosen intervals will never be an octave, any pairs of intervals of that supply will never be an octave and there will never occur diminished chords from these intervals."
© 2000, zuletzt geändert am 11. Februar 2000.

