Beiträge zur Elektronischen Musik 7
1.Der Diminutionsbegriff in der Musikgeschichte
Ich beziehe mich hier auf diverse Lexika, vornehmlich jedoch auf den Artikel 'Diminution' von Hans Engel.Dort werden folgende Bedeutungen des Diminutionsbegriffes unterschieden:
- Diminution als Bezeichnung. der Notationskunde: hier bezeichnet der Begriff die Möglichkeit, proportionale Verzerrungen der Notenwerte notationstechnisch darzustellen. Als Komplement erscheint hier die Augmentation.
- Diminution als Bezeichnung in der Fugenlehre: bedeutet das Erscheinen des Themas in verkürzten Werten.
- Diminution als Bezeichnung der Verzierungslehre.
Diminution leitet sich vom lat. 'diminuere' = zerspalten/zerkleinern ab:
"Diminution bedeutet [demnach] Zerkleinerung, Zerlegung
eines Tones in mehrere aufeinanderfolgende Töne, in eine Folge
von kürzeren Tönen".4
Zwischen dem 14. und 19. Jahrhundert ist Diminution ein
Synonym für Koloratur,Verzierungslehre und überhaupt für Ornamentik.
Diminutionen werden dabei vornehmlich durch
- Tonrepetition
- Umspielung eines Tones
- Ausfüllung eines Zwischenraumes von Tönen
Besonders die letztere Form wird für das Folgende wichtig werden.
Diminution war von Beginn der Musikgeschichte an ein
notwendiger Teil der Melodiebildung, keineswegs bloß zufällige
oder redundante Beigabe. Sie steht, etwa in der Entwicklung des
Organums, an der oft wenig beachteten Grenze zwischen Improvisation
und determinierter Komposition.
Improvisierte Diminution gehört so als unverzichtbarer
Bestandteil zur Gesangspraxis der Zeit.
Im 14. und 15. Jahrhundert findet eine Kanonisierung der Diminutionsformeln in den Lehrbüchern statt. Die verschiedenen Möglichkeiten der Diminution werden nach den auszufüllenden Melodieintervallen, den Diminutionsintervallen geordnet. Man kann hier bereits eine Erstarrung der ursprünglich frei gestalteten Diminutionen zu Formeln und Manieren feststellen.
Exemplarisch sei die Diminutionsschule "La Fontegara” von Silvestro Ganassi5 zitiert. Ganassi differenziert hier die Diminutionen nach dem Grad der Varietas, also des Variantenreichtums:

Abb. 1: Beispiel für eine Intervalldiminution aus "La Fontegara"
Ausgangspunkt ist bei Ganassi eine zu diminuierende Tonfolge
in längeren Werten, im obenstehenden Beispiel etwa in ganzen Noten.
Bemerkenswert ist die unterschiedliche metrische Unterteilung
der Ausgangswerte, wobei er u. a. Diminutionen der Zeitwerte in den
Proportionen 5:4,6:4,7:4 behandelt.
2.
Der Begriff der 'Selbstähnlichen Diminutionen'
Ich stieß bei der Lektüre von Allan Fortes 'Introduction to
Schenkerian Analysis' gleich zu Beginn auf den
Diminutionsbegriff, später auch auf das Konzept der Strukturebenen
Vorder-, Mittel-, und Hintergrund.
Der Diminutionsbegriff läßt sich einerseits also als
improvisatorische Intervallauffüllung im Vordergrund, also in
kleineren Werten, verstehen.
Andererseits bedeutet Diminution als Komplementärbegriff zur
Augmentation die proportional deformierte Kopie einer zeitlichen Gestalt.
Es stellt sich hier die zunächst spekulative Frage, ob nicht
eine Diminutionsform denkbar wäre, die beiden Auffassungen entspräche.
Anders formuliert: ist ein melodischer Verlauf vorstellbar, der
unabhängig von der betrachteten Strukturebe (eben Vorder-,
Mittel- und Hintergrund) die gleiche Gestalt zeigt. Die Ursprungsintervalle
der Diminution müßten dann in den rhythmischen und melodischen
Verkleinerungen der ausfüllenden und verzierenden ´passagi´
wieder erkennbar werden. Somit würde der Schenkersche Gedanke
realisiert werden, daß 'various aspects of large scale
structure are often mirrored in the small'.6
Ich möchte solche Diminutionsformen im weiteren als
'Selbstähnliche Diminutionen' bezeichnen.
Folgendes Beispiel aus einer weiteren Diminutionslehre von Antonio Brunelli soll den Gedanken verdeutlichen:7

Abb. 2: Beispiel für eine Diminution, welche die Ausgangsintervalle ähnlich wiederkehren lassen
Zuerst wird hier links die Ausgangsformel dargestellt, dann folgt rechts der Vorschlag für die Diminutionen; für mich war bei der Wahl dieses Beispieles wesentlich, daß die Diminutionen hier im speziellen der Gestalt der Ausgangsformel sehr ähnlich sind.
Ist die Möglichkeit eines solchen musikalischen Gebildes einmal demonstriert worden, läßt sich das Prinzip von drei auf beliebig viele Strukturebenen erweitern.
Die ähnliche Wiederkehr einer Gestalt auf verschiedenenr Strukturebenen zeigte für mich eine gewisse Affinität zur Struktur fraktaler Gebilde und Generatoren, wie sie von Mandelbrot und anderen mit dem Begriff Selbstähnlichkeit beschrieben wurden.
Ich will hier nochmals betonen, daß ich diese Affinität per analogiam, also im Sinne eines Übersetzungsversuches zwischen zwei an sich inkompatiblen Bereichen herstelle.
Ich will damit nicht die fraktale Struktur der von Schenker dahingehend untersuchten Werke behaupten. Vielmehr ging es mir um die kompositionstechnische Entwicklung eines Generators, der dieses Konzept in brauchbare musikalische Strukturen übersetzen könnte.
Fraktale Generatoren für kompositorische Zwecke stehen bereits in kommerzieller Musiksoftware zur Verfügung. Diese Generatoren projizieren Wertematrizen fraktaler Bilder auf die bescheidene Punktmenge von 128, 256 oder 512 Tonhöhen- oder Dauerwerten. Dabei bleibt die Frage bestehen, ob diese Transformationen jene Relationen von Selbstähnlichkeit, die in der fraktalen Geometrie so augenscheinlich werden, tatsächlich musikalisch auf eine wenigstens annähernd so evidente Weise repräsentieren können.
Ich suchte also nach einem Konstruktionsprinzip, das in
nicht-trivialer Weise komplexe Operationen wie selbstähnliche Diminutionen
mit einer begrenzten Tonmenge sinnvoll darstellen könnte.
Ich wollte zudem keinen vollständig determinierten
Algorithmus, der mich aller Entscheidungen über den
Kompositionsverlauf völlig enthob, sondern ein Verfahren, das
gegebenenfalls auch dem freien, improvisatorischen, ich möchte
etwas frei sagen, chaotischen Aspekt des Diminuierens Rechnung
tragen sollte.
Dabei war jener Aspekt, der Diminutionen als Ausfüllung eines
Intervalls auffaßt, Ausgangspunkt der Überlegungen. Diminution bedeutet
somit das Einfügen einer Tonreihe in ein Intervall I, deren
Rahmenintervall eben jenem Intervall I entspricht. Wir können von
einer Repräsentation des Intervalls durch die eingefügte Diminutionsreihe
sprechen, aber auch von einer Ersetzung und Substitution, da das
ursprüngliche Intervall in eben jenem Vorgang vordergründig
verschwindet. Forte betont, daß die Diminutionen die Bezugstöne
auch ersetzen, jene also explizit ebenfalls verschwinden können.8
Wir können zusammenfassend feststellen, daß die Summe aller Intervalle ik in der substituierenden Tonreihe gleich dem zu diminuierenden Intervall I ist.

Negative Zahlen bezeichnen hier nach unten gerichtete Sukzessivintervalle, positive bezeichnen Aufwärtsintervalle.
Der Diminutionsbegriff ist gleichzeitig untrennbar mit einer zeitlichen Strukturschichtung verbunden, welche die Dauer der Grundintervalle von denen der Diminutionsintervalle deutlich trennt. Das äußert sich in der Schenkeranalyse durch Differenzierung verschiedener Räumlichkeiten (Vorder/Mittel/Hintergrund).
Zwei von Forte erwähnte Etymologien scheinen mir in diesem Zusammenhang erwähnenswert:
1) die englische Übersetzung mit divisions = Teilungen, sowie die
2) Übersetzung des Diminutionsvorganges mit 'breaking the
ground', also mit Brechung.
Hier wird Diminution als Teilungsvorgang verstanden, als die
Aufteilung oder Brechung eines räumlichen Verhältnisses.
Als nächstes soll gezeigt werden, wie sich selbstähnliche
Diminutionen von Reihen als Algorithmus eines Strukturgenerators innerhalb
eines Kompositionsprogramms implementieren lassen.
3.
Die algorithmische Realisation der selbstähnlichen Diminutionen
Der dargestellte Algorithmus für selbstähnliche Diminutionen
von Reihen ist ein Modul aus meinem seit einigen Jahren in Entwicklung
begriffenen Programm "CADMUS Computer aided Construction
for Musical Applications”, das eine Reihe von Analysewerkzeugen
und Strukturgeneratoren für kompositorische Aufgaben zur
Verfügung stellt.
3.1 Über das Verhältnis Komposition Kompositionsprogramm
Dieses Modul entstand in Wechselbeziehung zum kompositorischen Prozeß und fand in mehreren meiner Stücke unmittelbare Anwendung.9Dabei stellte sich mir zunächst die Frage, ob es sinnvoll sei, sich als Komponist mit der programmtechnischen Entwicklung eines Algorithmus selbst zu beschäftigen, da dies doch mit enormen Zeitaufwand verbunden ist und dennoch wegen der meist geringen technischen Vorkenntnisse des Komponisten auf einfache Applikationen beschränkt bleiben muß.
Ich bin der Meinung, daß es relativ schwierig ist, in einem kommerziellen Kompositionsprogramm (seien sie auch noch so komplex und umfangreich wie etwa MAX10) jene Differenzierung und Individualisation der Lösungswege wiederzufinden, wie sie im Kompositionsprozeß auftreten müssen.
Zudem kann es beim Gebrauch fertiger Programme leicht zur unreflektierten Übernahme eines im Hintergrund der Programmstruktur vorhandenen Kategoriensystems kommen, was oft auch die unbewußte Übernahme von Auswahl und Bewertungskriterien bedeutet.
Es erscheint mir daher zweckmäßiger und von individuellerem Gehalt, als Komponist Programmierarbeit und Komposition zu verbinden, wobei der Weg der Lösungsfindung in beiden Bereichen oft sehr ähnlich sein kann; das schließt eine intensive Zusammenarbeit mit professionellen Programmierern keineswegs aus, vielmehr ist diese die Voraussetzng für eine eigene effektive Arbeit. Unterstützt wird diese Möglichkeit des Selbstprogrammierens durch die zunehmend leichtere Handhabbarkeit der Programmiersprachen.
Zurück zum Algorithmus für selbstähnliche Diminutionen von Reihen:
3.2 Entwicklung des Algorithmus im Kompositionsprozeß
Bei der Entwicklung des vorliegenden Algorithmus für selbstähnliche Diminutionen von Reihen ging ich zunächst von der Transposition eines Modells um die modelleigenen Intervalle aus. So verwendete ich als globales und lokales Organisationsprinzip in 'Modern Monsters'11 eine Abfolge der Reihen, deren Transpositionsintervalls die Reihe selbst bildeten. Die Abbildung 3 zeigt die Anwendung dieses Prinzips auf die Reihe aus ´Brüche´.12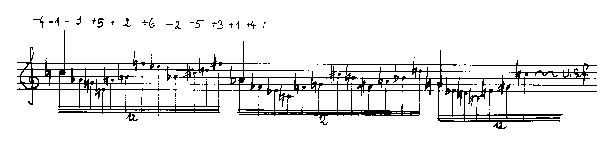
Abb. 3: Beispiel für eine Transposition einer Reihe um die reiheneigenen Intervalle (Hier um die ersten drei Intervalle -4, -1, -3)
Dieses Verfahren konnte kaum Gebilde größerer Komplexität als jene der klassischen Dodekaphonie und des Serialismus erzeugen. Bei der Weiterentwicklung ging ich von der spezifischen ästethischen Prämisse aus, nämlich aus ursprünglich einfachen Zellen umfangreiche, komplizierte und variable Gebilde wachsen zu lassen. Diese Prämisse läßt sich in folgenden Forderungen formulieren:
- Einfachheit der Ausgangsgestalt.
- Komplexitätswachstum für jede Stufe der Materialentwicklung
- Varietas
Hier führte mich die Lektüre der Bücher von Peitgen/Jürgens/Saupe13 durch ihre faßliche Einführung in die Gedanken Benoit Mandelbrots wesentlich weiter. In der Diskussion des Küstenlinienproblems stellt Mandelbrot die beiden Größen des Abstandes zwischen Ausgangs und Endpunkt einer Linie einerseits und der Summe aller gerasterten Einzelteile der Linie andererseits einander gegenüber, wobei zur Abstandsmessung jeweils verschiedene Scalings bzw. Rastergrößen verwendet werden. Die Analogiebildung zwischen Scaling und Diminutionsebene einerseits, zwischen graphischem und musikalischem Intervall andererseits lag nahe.
Ich fand weiters bei Mandelbrot in der Diskussion der Peano Kurve sowie bei Hans Hahn14 das Verfahren der iterativen Ersetzung räumlicher Intervalle durch verkleinerte Kopien der Ausgangsgestalt:
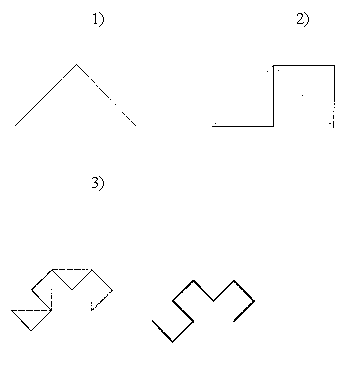
Abb. 4: Konstruktion einer Peano-Kurve
Die Abbildung zeigt drei Iterationen einer Peano - Kurve. Die
dabei entstehenden Strecken werden immer wieder durch verkleinerte
Kopien des Generators substituiert.15
Die Peano Kurven werden bei Mandelbrot als Füllkurven einer
Ebene bezeichnet, insofern sie diese mit fortschreitender Iteration sukzessive
ausfüllen.16 Auch hier war die Analogiebildung zum
intervallfüllenden Aspekt der Diminution naheliegend.
In den Peano - Kurven werden durch sehr einfache Generatoren
hochkomplexe Gebilde zur Anschauung gebracht, wobei für mich der
Aspekt der Fasslichkeit und Anschaulichkeit des agierenden
Prinzips richtungsweisend war. Das Problem war nun, inwiefern diese
Fasslichkeit im Falle einer Übertragung auf musikalische Parameter
nicht verlorengehen mußte oder andererseits zu trivialen musikalischen
Ergebnissen führte, die von der Leistungsfähigkeit und
Komplexität des Generators nichts hörbar werden ließen.
Diese Dialektik von Fasslichkeit und Intransparenz sollte also
in der Lösung nicht verschwinden, sondern als Bewegung im Hörer erhalten
bleiben.
Ich versuchte nun, jedes Intervall einer Tonfolge17 durch eine Kopie der Tonfolge selbst zu ersetzen. Dies läßt sich jedoch nur unter bestimmten Voraussetzungen bewerkstelligen:
Die Ausgangsreihe hat ein Summenintervall SI, das sich aus der Summe der Einzelintervalle zusammensetzt. Dieses Summenintervall kann ein Intervallquantum zunächst nur dann ersetzen, wenn dieses auch als Binnenintervall der Ausgangsreihe erscheint:
[4 13 +5 +2 ] SI = [-1]
Die Reihe könnte also das zweite Intervall der Reihe selbst ersetzen:
[4 [4 1 3 +5 +2] 3 +5 +2]
Um aber die restlichen Intervalle ersetzen zu können, müßte die Ausgangsreihe verändert werden, um eine Substitutionsreihe mit dem passenden Summenintervall herstellen zu können. So könnte die Reihe um den Faktor 4 proportional augmentiert werden, um das Intervall [-4] ersetzen zu können:
[[16 4 12 +20 +8] 1 3 +5 +2]
Diese proportionalen Ersetzungen haben den Nachteil, daß die
Grundgestalt stark deformiert wird, die Ähnlichkeitsbeziehungen weitgehend
verschwinden. Es können auch mikrotonale Diminutionen bzw.
Augmentationen von Intervallen notwendig werden, etwa bei der
Augmentation 5:3 einer Reihe mit dem Summenintervall [3] zu einer
Substitutionsreihe für das Intervall [5].
Außerdem gibt es dabei keine Variation der Gestaltfunktion,
das heißt der grundlegenden Bewegungsrichtungen der Intervalle unabhängig
von ihrer Größe. Länge und Form der Substitutionsreihe blieben
zudem gleich.
Das führte mich zum nächsten Lösungsvorschlag, nämlich der Verwendung von Partialreihen zur Substitution der Intervalle der Grundreihe.
4.
Partialreihen
4.1 Das Konzept der Partialreihe
Unter Partialreihe verstehe ich einen Ausschnitt einer Reihe. Die folgende Tabelle zeigt alle möglichen Partialreihen der bereits zitierten Reihe aus "Brüche”. In jeder Zeile sind die Ordnung O (=Länge), das Summenintervall SI und die Glieder der jeweiligen Partialreihe angegeben.
| O. | SI | Partialreihe | O. | SI | Partialreihe |
| 2 | [-5] [-4] [2] [7] [8] [4] [-7] [-2] [4] [5] |
[-4 -1] [-1 -3] [-3 5] [5 2] [2 6] [6 -2] [-2 -5] [-5 3] [3 1] [1 4] |
3 | [-8] [1] [4] [13] [6] [-1] [-4] [-1] [8] |
[-4 -1 -3] [-1 -3 5] [-3 5 2] [5 2 6] [2 6 -2] [6 -2 -5] [-2 -5 3] [-5 3 1] [3 1 4] |
| 4 | [-3] [3] [10] [11] [1] [2] [-3] [3] |
[-4 -1 -3 5] [-1 -3 5 2] [-3 5 2 6] [5 2 6 -2] [2 6 -2 -5] [6 -2 -5 3] [-2 -5 3 1] [-5 3 1 4] |
5 | [-1] [9] [8] [6] [4] [3] [1] |
[-4 -1 -3 5 2] [-1 -3 5 2 6] [-3 5 2 6 -2] [5 2 6 -2 -5] [2 6 -2 -5 3] [6 -2 -5 3 1] [-2 -5 3 1 4] |
| 6 | [5] [7] [3] [9] [5] [7] |
[-4 -1 -3 5 2 6] [-1 -3 5 2 6 -2] [-3 5 2 6 -2 -5] [5 2 6 -2 -5 3] [2 6 -2 -5 3 1] [6 -2 -5 3 1 4] |
7 | [3] [2] [6] [10] [9] |
[-4 -1 -3 5 2 6 -2] [-1 -3 5 2 6 -2 -5] [-3 5 2 6 -2 -5 3] [5 2 6 -2 -5 3 1] [2 6 -2 -5 3 1 4] |
| 8 | [-2] [5] [7] [14] |
[-4 -1 -3 5 2 6 -2 -5] [-1 -3 5 2 6 -2 -5 3] [-3 5 2 6 -2 -5 3 1] [5 2 6 -2 -5 3 1 4] |
9 | [1] [6] [11] |
[-4 -1 -3 5 2 6 -2 5 3] [-1 -3 5 2 6 -2 -5 3 1] [-3 5 2 6 -2 -5 3 1 4] |
| 10 | [-2] [10] |
[-4 -1 -3 5 2 6 -2 -5 3 1] [-1 -3 5 2 6 -2 -5 3 1 4] |
11 | [6] | [-4 -1 -3 5 2 6 -2 -5 3 1 4] |
Diese Teilreihen repräsentieren damit die Teilsummenintervalle, die innerhalb der Reihe auftreten.
Durch die Verwendung von Partialreihen zur Intervalldiminution wird eine Vielfalt von Ersetzungsmöglichkeiten für die Ausgangsintervalle geschaffen. Für manche Ausgangsintervalle stehen mehrere Substitutionsreihen zur Verfügung. So tritt z.B. das Summenintervall [+2] bei Partialreihen der Ordnung 2,4,7 und 10 auf. Kriterien für die individuelle Auswahl werden in Abschnitt 4.3. diskutiert werden.
4.2 Varianten
Die Partialreihe kann zusätzlich unterschiedlich generiert werden.Werden dazu wie oben ausschließlich die richtungskonstanten Ausgangsintervalle verwendet, ohne Komplementärintervalle einzubeziehen, spreche ich von authentischen Partialreihen.Bei einer zyklisch verstandenen Reihengestalt mit einem zusätzlichen Schlußintervall, das wieder zum Anfang führt, können entsprechende zyklische Partialreihen gebildet werden. Das Schlußintervall entspricht der Umkehrung des Summenintervalles. Dadurch kommt es zu einer weiteren Vergrößerung der Vielfalt substituierbarer Intervalle:
Ausgangsreihe: [4 1 3 +5 +2 ] Schlußintervall: [+1]
Diese Sechstonreihe mit dem
Schlußintervall [+1] hat folgende zyklische Partialreihen der Ordnung 2:
[4 1]=[5]
[1 3]=[4]
[3 +5]=[+2]
[+5 +2]=[+7]
[+2+1]= [3]
[+1 4] [3]
Durch die zyklische Interpretation vergrößert sich hier die Menge der möglichen Substitutionsintervalle um die Elemente [+3] und [3].
In der authentischen Partialreihe sind die Ähnlichkeitsrelationen am stärksten ausgeprägt. Vermindert werden sie durch Einbeziehung von Komplementärintervallen, etwa durch Darstellung der Ausgangsreihe in ausschließlich positiven Intervallen. Ich nenne diese Transformationen plagale Partialreihen, also Ableitungen aus der Grundreihe. Sie lassen sich weniger in der linearen Diminution verwenden als in der vertikalen bzw. harmonischen, über die noch zu sprechen sein wird. Die folgende Tabelle zeigt die plagalen Partialreihen der Reihe aus 'Brüche'.
| O. | SI | Partialreihe | O. | SI | Partialreihe |
| 2 | [19] [20] [14] [7] [8] [16] [17] [10] [4] [5] |
[8 11] [11 9] [9 5] [5 2] [2 6] [6 10] [10 7] [7 3] [3 1] [1 4] |
3 | [28] [25] [16] [13] [18] [23] [20] [11] [8] |
[8 11 9] [11 9 5] [9 5 2] [5 2 6] [2 6 10] [6 10 7] [10 7 3] [7 3 1] [3 1 4] |
| 4 | [33] [27] [22] [23] [25] [26] [21] [15] |
[8 11 9 5] [11 9 5 2] [9 5 2 6] [5 2 6 10] [2 6 10 7] [6 10 7 3] [10 7 3 1] [7 3 1 4] |
5 | [35] [33] [32] [30] [28] [27] [25] |
[8 11 9 5 2] [11 9 5 2 6] [9 5 2 6 10] [5 2 6 10 7] [2 6 10 7 3] [6 10 7 3 1] [10 7 3 1 4] |
| 6 | [41] [43] [39] [33] [29] [31] |
[8 11 9 5 2 6] [11 9 5 2 6 10] [9 5 2 6 10 7] [5 2 6 10 7 3] [2 6 10 7 3 1] [6 10 7 3 1 4] |
7 | [51] [50] [42] [34] [33] |
[8 11 9 5 2 6 10] [11 9 5 2 6 10 7] [9 5 2 6 10 7 3] [5 2 6 10 7 3 1] [2 6 10 7 3 1 4] |
| 8 | [58] [53] [43] [38] |
[8 11 9 5 2 6 10 7] [11 9 5 2 6 10 7 3] [9 5 2 6 10 7 3 1] [5 2 6 10 7 3 1 4] |
9 | [61] [54] [47] |
[8 11 9 5 2 6 10 7 3] [11 9 5 2 6 10 7 3 1] [9 5 2 6 10 7 3 1 4] |
| 10 | [62] [58] |
[8 11 9 5 2 6 10 7 3 1] [11 9 5 2 6 10 7 3 1 4] |
11 | [66] | [8 11 9 5 2 6 10 7 3 1 4] |
Neben den plagalen Partialreihen kann die Vielfalt der möglichen Substitutionen weiters durch Variationen in der Ausgangsreihe erhöht werden.
So können etwa bei der Untersuchung von Allintervallreihen bei einer vorgegebenen Anfangsserie von z.B. 4 Tönen verschiedene Lösungen für die Resttöne der Reihe gefunden werden, die kleine Variationen ergeben. Dieses können ihrerseits wiederum partialisiert werden, wodurch neue Substitutionsintervalle entstehen und somit die Vielfalt vergrößert wird.
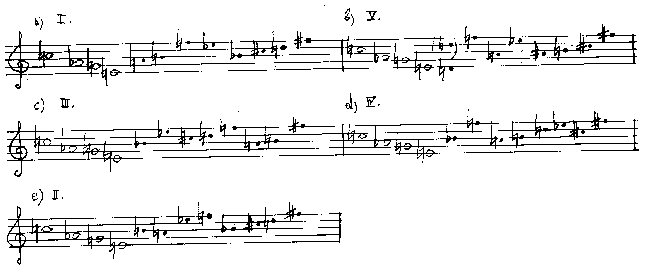
Abb. 5: Ergänzung einer viertöigen Ausgangsreihe zu verschiedenen zwölftöigen Allintervallreihen
Die Abbildung zeigt Variantreihen zu einem gegebenen fixen Ausgangsmodell CAbGE, wobei die ´Verwandtschafts´bzw. Ähnlichkeitsgrade von mir römisch beziffert wurden. Alle fünf Reihen sind übrigens Allintervallreihen und stellen alle Lösungen für diesen Fall dar. Diese Reihen können eine Vielfalt von unterschiedlichen, aber verwandten Partialreihen erzeugen.
Wesentlich ist nun, daß Grundgestalt und Krebs jeder Partialreihe summengleich sind, sowie Grundgestalt und Umkehrung, mit dem Faktor 1 multipliziert, summengleich sind. Alle diese Transformationen können zur Substitution verwendet werden, da die vier 'klassischen' Transformationen, solange man die Quantität und Richtung der auftretenden Intervalle innerhalb der jeweiligen Reihenform unangetastet läßt, die Ähnlichkeitrelationen erhalten.
Ich meine, daß es eben diese
Ähnlichkeitsrelationen sind, welche in der Entwicklung der
Reihentechnik über die Verwendbarkeit einer Transformation
entschieden haben.
Abstraktion und
Anschaulichkeit (d.h. hörbare Faßlichkeit) stehen hier in einem
geschichtlich entwickelnden dialektischen Spannungsfeld.
4.3 Die Diminution einer Reihe mittels Partialreihen
Ist das Feld der möglichen Ersetzungen der Ausgangsintervalle einmal abgesteckt, hier in Form einer Tabelle über alle möglichen Partialreihen, kann eine erste Ersetzung stattfinden. Da für einige Intervalle mehrere Lösungen existieren, muß eine Auswahl getroffen werden.4.3.1 Frei gewählte Diminution
Die Auswahl der jeweiligen Partialreihe für jedes zu substituierende Intervall kann vom Komponisten getroffen werden, wobei folgende Kriterien ausschlaggebend sein können:
- Die optimale Vermeidung von Sequentiellem durch geschickte Verwendung sich einander ergänzender Partialreihen (Komplementaritätskriterium) und durch abwechselnde Verwendung der vier Grundtransformationen G, K, U, UK der Partialreihen.
- Das gewünschte Wachstum der resultierenden Reihe: Je nach der Länge L der verwendeten Partialreihe wird mit jeder Diminution ein Zuwachs von L-1 Tönen erreicht. Geht man von einer bestimmten gewünschten Länge der Zielreihe aus, laßt sich diese durch Kombination verschiedener Partialreihenlängen erzielen.
- Einbeziehung der erreichbaren absoluten Tonhöhen: Jede Substitution fügt neue Töne in die Ausgangsreihe ein. Man wird also trachten, möglichst viele verschiedene neue Punkte zu gewinnen, was von der verwendeten Partialreihe und ihrer Grundtransformation abhängt (Varietas in der absoluten Reihe). Diese Forderung entspringt dem intuitiven Verständnis einer 'raumfüllenden Kurve' also dem möglichst vollständigen und variablen Ausfüllen des Tonhöhenraums.
4.3.2 Deterministische Diminution
Die Auswahl der substituierenden Partialreihen kann von vornherein deterministisch in einer 'Substitutionstabelle' festgesetzt werden. Die Ersetzungen folgen dann immer diesem Schema. Diesen Vorgang habe ich auch als Modul im Programm CADMUS implementiert. Er eignet sich für die Untersuchung des Entwicklungsverhaltens und Wachstumsprozesses einer solchermaßen generierten Makro Reihe.Die Substitutionstabelle kann
z.B. lauten:
| Summe | Ordnung | Ersetzung |
| -4 -1 -3 5 2 6 -2 -5 3 1 4 -6 |
5 5 5 6 4 5 4 6 5 5 5 5 |
[-2 -6 2 5 -3] [-4 -1 -3 5 2] [-6 2 5 -3 -1] [2 6 -2 -5 3 1] [6 -2 -5 3] [5 2 6 -2 -5] [-3 5 2 -6] [-1 -3 5 2 -6 -2] [1 3 -5 -2 6] [-2 -5 3 1 4] [3 -5 -2 6 2] [5 2 -6 -2 -5] |
4.3.3 Stochastische Diminution
Die Auswahl der substituierenden Partialreihen kann auch durch einen Zufallsgenerator erfolgen, wobei hier zusätzliche Filter einzuschalten wären, die vor allem in den für das Gehör transparentesten Schichten triviale Wendungen und gehäufte Wiederholungen ausgrenzen. Besonders bei der Substitution sehr großer Tonmengen wird diese Form der Diminution sinnvoll und nützlich.18-----------------------------------------------------------------------
4 Engel, MGG, S. 489
5 Venedig 1535
6 Vgl. Forte, ISA, S 235 f
7 Vgl. Antonio Brunelli, Varii Esercitii 1614, S. 4
8 Vgl. Forte, a.a.o., S.9
9 Lang, "Quartett für Flöte", Graz 1990
Lang, "Brüche für Sextett", Graz 1991
Lang, "Küstenlinien für 2 Klaviere und 2 Schlagwerker", Graz 1992
Lang, "La - bas a S" für tiefes Orchester, Graz 1993
Lang, "Feld - Studie" für Streichorchester", Graz 1994
10 Bei MAX handelt es sich um eine objekt-orientierte Entwicklungsumgebung für Echtzeitapplikationen.
Sie wurde 1987 von Miller Puckette am IRCAM, Paris, entworfen und später von David Zicarelli weiterentickelt. Die Software existiert
in zwei unterschiedlichen Varianten: in einer mit Klangverarbeitungsfunktionen angereicherten Fassung dient sie als Benutzeroberfläche der ISPW,
während die von OPCODE Ltd. vertriebene stark erweiterte MacIntosh-Version in erster Linie für die Generierung und Manipulation von MIDI-Daten Verwendung findet.
11 Lang, "Modern Monsters" für Violoncello und Klavier, Graz 1990
12 Vgl. Fußnote 9. Diese Reihe wird im folgenden als Beispiel verwendet werden: [-4 -1 -3 +5 +2 +6 -2 -5 +3 +1 +4]. Es handelt sich übrigens um eine
krebsgleich Allintervallreihe.
13 Siehe Literaturverzeichnis
14 Vgl. Hahn, Die Krise der Anschauung.
15 Vgl. Mandelbrot, FGN, S. 78 ff
16 Vgl. Mandelbrot, a.a.o., S 71
17 also einer relationalen Reihe im Gegensatz zu einer absoluten Reihe aus Tonhöhen oder Frequenzen.
18 Der Verweis auf stochastische Diminution wurde von Robert Hödrich angeregt.
© 2000, zuletzt geändert am 11. Februar 2000.

