Beiträge zur Elektronischen Musik 7

5. Iteration des Substitutionsprozesses

Der oben beschriebene Vorgang der Substitution läßt sich iterativ wiederholen; das heißt, die Substitutionen werden an jedem Intervall der neugewonnenen Reihe ausgeführt, was wieder zu einer neuen Makroreihe führt und so fort. Es kann hierbei in allen Iterationen dieselbe Substitutionstabelle verwendet werden, aber auch Variationen derselben.

Die Länge der Reihe wächst dadurch exponentiell. Deshalb habe ich bisher auch meist nur 3 ­5 Iterationsebenen verwendet, was immerhin zu Reihenlängen von über tausend Tönen führte. Diese Iterationsebenen legen in der Realisation eine musikalisch­strukturelle Abschattung nahe, um die Vielschichtigkeit des Ergebnisses auch hörbar zu machen.

In diesem Vorgang wird, so meine ich wenigstens, die Affinität zu den Iterationen der Patterngeneratoren bei Mandelbrot besonders deutlich.

Das folgende Beispiel zeigt 5 Interationsebenen aus 'Brüche' (Abb. 6 und 7). Als Substitutionstabelle wurde für Iteration I­IV verwendet:

Summe	Ordnung	Ersetzung
-4 -1 -3 5 2 6	2 3 4 2 2 3	[-6 2] [1 3 -5] [-4 1 3 5] [1 4] [-3 5] [2 6 -2]

Für die V. Iteration wurden Mikrointervalle zur Diminution verwendet.

Die Substitutionstabelle lautet:

Summe	Ordnung	Ersetzung
-12(4) -3(-1) -9(-3) 15(+5) 6(+2) 18(+6)	4 -4 5 4 3 5	[-4 -1] + [-2 -5] [-4 -1 -3 5] [1 3 -5 -2 -6] [5 2] + [2 6] [2 6 -2] [1 4] + [5 2 6]

Die V. Iteration wurde in Abb.6 aus Platzgründen nicht mehr vollständig ausgeführt.

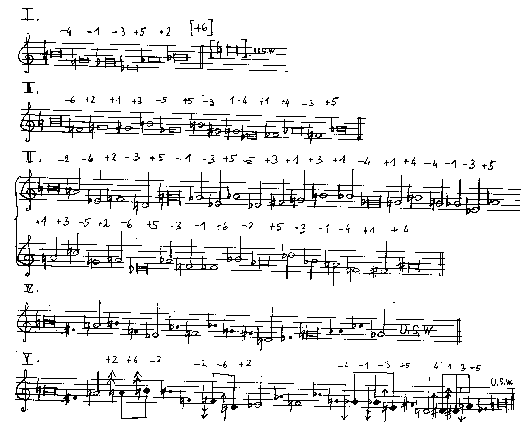
Abb. 6: Iterative Diminution aus 'Brüche': Konstruktionsplan

Hier wird mit Sechsteltönen substituiert. Die halbtönigen Intervalle werden dementsprechend verdreifacht. In der Substitutionstabelle nicht auftretenden Intervalle werden durch Addition mehrerer ersetzbarer Intervalle diminuiert.
Die deterministische Verwendung obenstehender Substitutionstabelle führte zu folgenden musikalischen Ergebnissen (ein Beispiel einer Klarinettenstelle aus ´Brüche´ soll einen Diminutionsvorgang mit Lizenzen verdeutlichen):

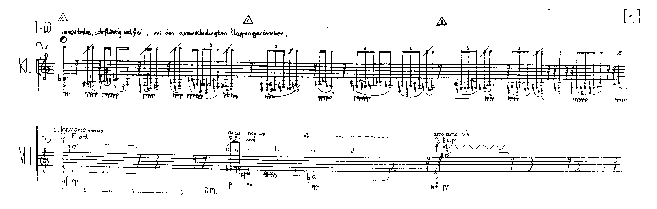
Abb. 7: Partiturausschnitt aus 'Brüche', T.1ff

6. Strukturelle Darstellung der Iterationsebenen

Um die Iterationsebenen unterschiedlich darstellen zu können, bieten sich verschiedene Möglichkeiten an:

6.1. Zeitliche Differenzierung

Im Begriff der Diminution an sich ist die zeitliche Differenzierung bereits enthalten, wobei die zu diminuierenden Ausgangswerte mit den unterscheidbar längeren Zeitwerten assoziiert werden, den Diminutionen selbst werden kürzere Bewegungen zugeordnet. Im vorliegenden Algorithmus kann dementsprechend die Zeiteinheit pro Iterationsebene verkleinert werden. Außer der substraktiven Verkleinerung bei gleichbleibender metrischer Einheit ist auch eine Verkleinerung der letzteren möglich. Als Beispiel:

Iterationsebene 0	--->	metrische Teilung	1:4
Iterationsebene 1	--->	metrische Teilung	1:5 bzw. 1:10
Iterationsebene 2	--->	metrische Teilung	1:6 bzw. 1:12 u.s.f

6.2. Dynamische Differenzierung

Die dynamische Differenzierung der Iterationsebenen würde einer neuen, freieren Art von dynamischer Serialisierung gleichkommen und ist mehrfach variierbar. Jeder Iterationsebene wird hier ein dynamischer Bereich zugeordnet. Als Beispiel:

Iterationsebene 0	--->	pppppp bis ppp
Iterationsebene 1	--->	ppp bis p
Iterationsebene 2	--->	p bis mf
Iterationsebene 3	--->	mf bis f
Iterationsebene 4	--->	f bis ff

Ebenso denkbar ist eine Umkehrung der Zuordnung, also die Iterationsebene 0 mit den f/ff Werten zu belegen.

6.3. Klangliche Differenzierung

Klangliche Differenzierung ist natürlich mit der dynamischen eng verbunden. Möglich sind darüber hinaus Zuordnungen von:

• Spieltechniken (z.B.: arco, pizz, col legno, sul ponticello, sul tasto etc.)
• Instrumentation: Verteilung der Ebenen auf verschiedene Instrumente/ Instrumentengruppen
• Präparationen: Ausklammerung oder Unterstreichung einzelner Ebenen durch Präparation der betroffenen Töne.

6.4. Differenzierung durch mikrotonale Diminutionen

Die Intervallbeziehungen der iterationsspezifischen Diminutionen können in verschiedenen Oktavteilungen dargestellt werden:

Iterationsebene 0	--->	Teilung pro Oktave	1:12 ( Halbtöne)
Iterationsebene 1	--->	Teilung pro Oktave	1:24 (Vierteltöne)
Iterationsebene 2	--->	Teilung pro Oktave	1:48 (Achteltöne)

Die Substitutionsmöglichkeiten schränken sich bei dieser Wahl natürlich ein.
Das Intervall 3 (kleine Terz) der Iterationsebene 0 würde einem Intervall 6 (sechs Vierteltöne) der Iterationsebene 1 entsprechen. Es kämen dann alle Substitutionen für den Wert [6] in Frage. In der Achteltonebene käme es zu einer weiteren Verdopplung der Ausgangswerte, was hier schon zum relativ ungünstigen Wert [12] führen würde.

6.5. Differenzierung durch unterschiedliche Freiheitsgrade im Diminutionsvorgang

Bisher wurde die Betrachtung auf einen mehr oder weniger determinierten Automaten eingeschränkt; tatsächlich laßt sich die Diminution natürlich auch in einem freien Nachempfinden der Ausgangsintervallik improvisatorisch durchführen. Dabei bleibt die Gestaltfunktion der diminuierten Reihe bzw. ihr Gestus annähernd erhalten, vor allem, wenn sich die freie Diminution auf die letzte Strukturebene beschränkt und die Ausgangsintervallik der tieferen Strukturebenen beläßt.

6.6. Differenzierung nach Verzerrungsgraden

Derzeit arbeite ich an der Entwicklung von Verzerrungsprozessen im Iterationsvorgang: mit jedem Iterationsschritt soll die Substitutionstabelle durch einen 'zufälligen' Faktor deformiert werden. Dadurch steigt die Varietas, allerdings führt dieser Vorgang sehr schnell zu einem völligen Schwinden aller Ähnlichkeitsbeziehungen. Denkbar wären hier diskret anwachsende proportionale Verformungen der Ausgangsintervallik mit jeweils neuen Partialisierungen und Substitutionen pro Iteration. Dadurch würde es zu einer langsam fortschreitenden Entfernung von der Grundgestalt kommen.

Spätestens hier muß der Einwand auftreten, ob es sich bei dem beschriebenen Verfahren nicht einfach um ein neoserialistischens Paradigma handle. Als Ausgangspunkt würde ich diese Klassifikation bejahen, doch in der Dynamik des Iterationsvorganges kann es zu einer neuen Auffassung der Serie an sich kommen, die als Metaserie

a) die Merkmale einer Binnenkontrapunktik zeigt, also in sich kein einschichtiges Gebilde darstellt,
b) sich nicht auf dodekaphonische Vollständigkeit und Komplementarität beschränkt,
c) authentisch in ihrem Umgang mit richtungsgleichen Intervallen sein kann,
d) verschiedene Freiheitsgrade des Komponierens simultan integrieren kann,
e) deren Umfang sehr groß werden kann,
f) und die letztlich auch harmonische Deutungen zuläßt.

Andererseits läßt sich das Verfahren bei einer strengen Konzeption der Diminutionsregeln als serielles Verfahren verstehen, d.h., sie schließt diese Deutung nicht aus, kann sie aber vielleicht erweitern.
Ich sehe so etwa die Möglichkeit, unter Verwendung deterministischer Prozesse einen Zufallsgenerator im Sinne Cage´s zu schaffen, vor allem bei Erzeugung größerer Tonmengen. Durch mehrfache Iteration läßt sich der Tonraum sehr schnell mit Klangmassen ausfüllen, was besonders unter Verwendung von Mikrointervallik einer Annäherung an das Rauschen entspricht.

7. Harmonische bzw. vertikale Diminutionen

Bislang wurde nur die Diminution von Sukzessivintervallen diskutiert. Dadurch laßt sich eine 'selbstähnliche' Struktur in der horizontal-melodischen Dimension herstellen. Es stellt sich nun die Frage, ob der gleiche Vorgang in der vertikal­harmonischen Dimension ebenfalls zu bewerkstelligen ist.

Die Ausgangsreihe laßt sich zunächst auf verschiedene Weisen seriell ­harmonisch interpretieren:

7.1. Harmonische Deutungsmöglichkeiten der Reihe

7.1.1 Kontraktionsklang

Ein Kontraktionsklang entsteht durch: Zusammenziehung aller Sukzessivintervalle zu Simultanintervallen. Die Ähnlichkeitsbeziehung zur Grundgestalt geht dabei weitgehend verloren. Es treten neue Intervallstrukturen in der Vertikale auf.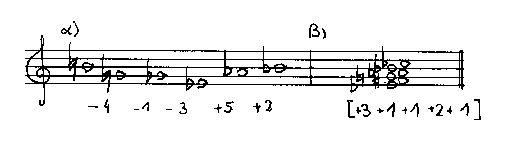

Abb. 8: Kontraktion von fünf Sukzessivintervallen zu einem sechstönigen Akkord

7.1.2. Akkord der Positivintervalle

Hierbei treten alle Intevalle der Reihe in ihrer positiven Form auf, [-4] wird also zum dodekaphonischen Komplement [8], [-1] zum Komplement [11] u.s.f. Hier gibt es Ähnlichkeitsbeziehungen zur Grundgestalt, allerdings mit der Einschränkung der Gleichsetzung von Komplementärintervallen, die eine starke Verformung der Grundgestalt bewirkt. Die Intervalle können in der vertikalen Interpretation sowohl von unten nach oben als auch umgekehrt aufgetragen werden.¹⁹

ABB.9: Positivintervallakkord der Reihe [-4-1-3+5+2]

7.1.3. Akkord der Absolutbetragsintervalle

Behält man die Intervalle in ihrer absoluten Quantität bei und trägt sie in der Vertikalen auf, erhält man einen Akkord, der wieder Ähnlichkeit zur Ausgangsreihe zeigt: So wird die Ausgangsreihe [-4-1-3+5+2] zum Akkord [+4+1+3+5+2].

ABB.10: Akkord aus den Absolutbeträgen der Reihe [-4-1-3+5+2]

7.1.4. Proportionalteilungsakkord der Positivintervalle

Die in 7.1.2. erwähnten Positivintervalle können auch als Proportionen einer Teilung eines Rahmenintervalls interpretiert werden. Im Fall der Reihe [-4-1-3+5+2] wären das die Proportionen 8:11:9:5:2. Angenommen das Rahmenintervall sei 1300 cent, also eine kleine None im temperierten System, so erhielte man durch die Proportionalteilung einen Akkord mit den Intervallen:

297.14 c

408.57 c

334.29 c

185.71 c

74.29 c

Hier liegt bereits ein Beispiel für eine vertikale Diminution vor. Die Centwerte könnten einem Zwölfteltonsystem angenähert werden, um sie in Notenschrift darstellbar zu machen.
Der Einfachheit wegen führe ich hier ein weiteres Beispiel an, bei dem die Proportionalteilung ganze Centwerte ergibt und das somit in traditioneller Notenschrift darstellbar ist.

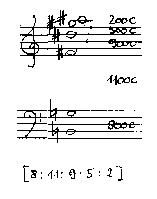ABB.11: Akkord aus den Proportionen der Positivintervalle

7.1.5. Als Proportionalteilungsakkord der Absolutbetragsreihe

Analog läßt sich die in 7.1.3 zitierte Absolutbetragsreihe als Proportionsreihe interpretieren. Ein Rahmenintervall von 1300 cent ergibt dann bei der Teilung 4:1:3:5:2 folgende Intervalle:

346.67 c

86.67 c

260 c

433.33 c

173.33 c

Das folgende Beispiel zeigt eine Approximation der Proportionsreihe mit Sechsteltonintervallen bei einem Rahmenintervall von 3500 cent:

ABB.12: Akkordteilung mit den Proportionen der Absolutbetragsreihe

Bei den letzteren Formen handelt es sich bereits um extreme Abstraktionen der Ähnlichkeitsbeziehungen.

7.2. Die Harmonische Matrix

Bereits in einer Verbindung mehrerer Akkorde kommt es zu einer Verknüpfung horizontaler und vertikaler Strukturbetrachtung. Die Tonhöhen werden so in einer Matrix darstellbar, deren Spalten den Einzelakkorden, deren Zeilen den individuellen Stimmverläufen entsprechen. ²⁰
Bei der harmonischen Diminution gehe ich zunächst von einem ´Gerüstsatz´ aus, also einer höchsten und einer tiefsten Schicht. Diese den Satz begrenzenden Melodieverläufe entnehme ich den Ergebnissen einer linearen Diminution.
Bei der folgenden vertikalen Diminution versuche ich das gleiche Reihenmaterial zu verwenden wie in der horizontalen, um der Prämisse der selbstähnlichen Organisation zu genügen. Die obere und untere Grenzlinie stellen in einem Satz Note gegen Note eine Menge von Rahmen- oder Füllintervallen her (Abb. 13). Gelingt es nun, diese Intervalle jeweils mit harmonisch interpretierten Partialreihen aus der Ausgangsreihe zu diminuieren, so ergibt sich eine Matrix, die in beiden Dimensionen ähnliche Strukturen zeigt.

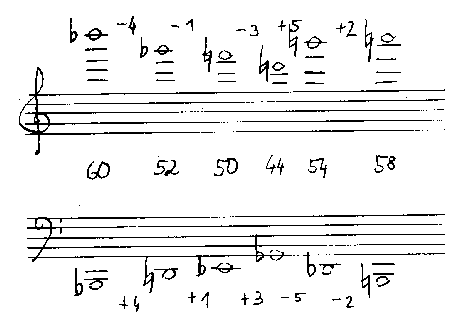
Abb. 13: Die Grenzlinien vor der Diminution mit der Menge der Rahmenintervalle

7.3 Die Diminution der Füllintervalle

Für die Diminution der Rahmenintervalle stehen folgende Möglichkeiten zur Auswahl:

7.3.1. Ausfüllung mit den harmonikalen Deutungsmöglichkeiten 7.1.1.­7.1.6

Hier sind Auswahlsentscheidungen zwischen den verschiedenen vertikalen Diminutionsformen zu treffen, wobei der Übergang von einem zum anderen Diminutionsakkord nach mehr oder weniger strengen traditionellen Kriterien (Stimmführung, Klangwiederholung, Liegetöne etc) ausgeführt werden kann. Ein weiterer freier Parameter ist die Anzahl der zu interpolierenden Töne, die von Klang zu Klang wechseln kann.

Die Formalisierung dieses Vorganges ist mir noch nicht befriedigend gelungen, weil die algorithmische Durchführung sehr komplex sein muß, wenn sie nicht zu trivialen Lösungen führen soll.

7.3.2. Additive Zerlegung des Füllintervalls

Oft stehen keine passenden Substitutionen in der Tabelle zur Verfügung, vor allem bei sehr großen Rahmenintervallen. In diesem Fall kann man das Rahmenintervall in mehrere substituierbare Intervalle zerlegen, wobei diese auch instrumentatorisch gesondert behandelt werden können, um die Aufteilung zu verdeutlichen.
In Abb. 14 wurde das Füllintervall jeweils durch die Addition zweier Substitutionen interpoliert, um dem großen Ambitus gerecht zu werden.

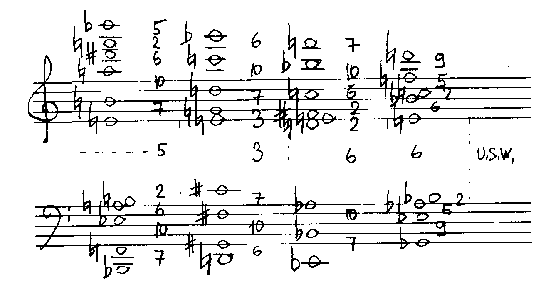
Abb. 14: Beispiel für eine harmonische Diminution der Rahmenintervalle aus Abb. 13

7.3.3. Iterative Diminution des Füllintervalls

Wurde einmal eine passende Diminution des Füllintervalls gefunden, so können die dabei entstehenden Intervalle wiederum durch weitere Diminutionen substituiert werden, was die Stimmzahl des Akkordes weiter erhöht.

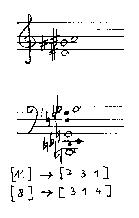ABB.15: Beispiel für eine iterierte harmonische Diminution: Die schwarzen Noten zeigen die aus der letzten Iteration hervorgegangenen Töne. Der Ausgangsakkord findet sich in der Abb. 9

8. Kombinationen von horizontaler und vertikaler Diminution: Die ´Raumfüllende Linie´

Die Vorstellung einer harmonischen Matrix wurde wesentlich durch die Konzeption des Hauerschen Zwölftonspiels einerseits, durch die Registrierungsharmonik Weberns andererseits angeregt. In beiden Modellen erschien es mir immer merkwürdig, daß die Ähnlichkeitsrelationen im vertikalen Bereich, nämlich der konstante Bezug auf die regelmäßige Abfolge von zwölf Tonhöhen-Klassen, im vertikalen Bereich chromatischen Bildungen bzw. Terzenstrukturen gegenüberstanden, die auf diese Abfolge keine Rücksicht nahmen. Aus dieser Überlegung heraus hatte ich versucht, auch die Akkorde mit einem reihenähnlichen- oder verwandten Intervallrepertoire zu füllen.
Diese harmonischen Diminutionen haben bereits gezeigt, daß sich die Trennung zwischer linearer und vertikaler Betrachtungsweise in der Matrix aufhebt. Daraus ergibt sich die Frage, ob sich eine weitere Diminutionsform finden ließe, die melodische mit harmonikaler Diminution kombinierte. Diese Diminution müßte sowohl die Intervalle der Akkorde mit der Ausgangsreihe ähnlichen oder gleichen Intervallfolgen ausfüllen als auch im Melodieverlauf auf einer der beschriebenen selbstähnlichen Diminutionen beruhen.

Der Determinationsgrad einer solchen Linie wäre nunmehr sehr hoch, die Lösungsmenge kann demnach nur sehr klein sein. Man könnte exakte Lösungen mit einem entsprechenden Suchprogramm finden. Gibt es keine derartige Lösung, so empfiehlt es sich praktisch, die resultierende Linie durch Ähnlichkeitstransformationen einzupassen, etwa durch:

8.1. Einpassung durch Intervallmodifikation

Um in der Matrix weiter entfernte Rasterpunkte melodisch zu erreichen, empfiehlt sich z.B die richtungsbeibehaltende Gleichsetzung der oktavvergrößerten Intervalle (Z.B: [1] =[ 13] , das heißt die kleine Sekund entspricht dann der kleinen Non im Zwölftonsystem). Wieder muß man hier wie auch bei allen anderen Ähnlichkeitsrelationen die mehr oder weniger weitgehende Abstraktion von der Grundgestalt in Kauf nehmen. Ansonsten gilt hier das bereits in 4.2 Gesagte.

8.2. Die Matrix als Näherung

Eine andere Lösung für eine die Matrix selbst diminuierende Linie liegt in einer approximativen Verwendung der Matrix, deren Werte dabei nur annähernd erreicht werden und bei genügend großer Häufung quasi einen 'Attraktor' bilden. Dies wird vor allem in mikrotonalen Matrizen bei größeren Tonmengen praktikabel, wobei sich dann anstatt der konkreten Punktwerte einer Tonhöhenmatrix Wertebereiche mit bestimmten Häufigkeitsverteilungen um diese Punkte ergeben.

Hier soll eine bloß schematische Skizze den Vorgang verdeutlichen:

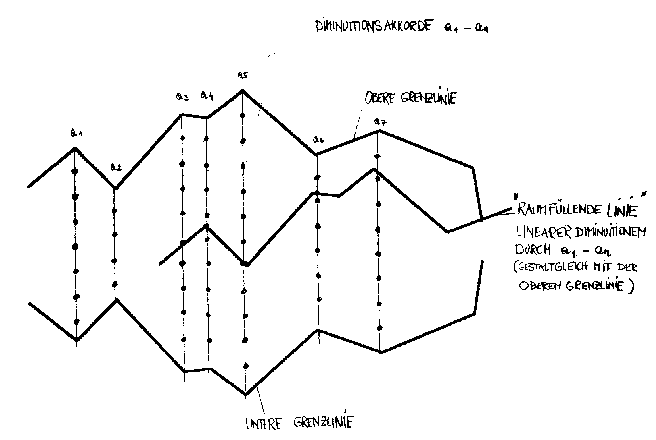
Abb. 16: Lineare Diminution einer harmischen Matrix

Die beiden dicken äußeren Linien repräsentieren die Grenzlinien, den Gerüstsatz der harmonischen Matrix. Beide sind aus einer selbstähnlichen iterativen Diminution hervorgegangen. Die vertikalen Strich - Punkt - Linien symbolisieren die Akkorde aus der harmonischen Diminution des Gerüstsatzes. Die dicke Linie zwischen den Grenzlinien zeigt eine kombinierte Diminution, die sowohl eine lineare Diminution durchführt als auch die Punkte der Akkordmatrix (annähernd) berührt.

Eine solchermaßen gewonnene Struktur hat die Eigenschaft, im strukturellen Hintergrund unter allen (musikalischen) Gesichtspunkten Ähnliches oder Gleiches zu zeigen, gleichzeitig aber im Vordergrund größte Vielfalt erscheinen zu lassen, was ja der Ausgangspunkt der Überlegungen war.²¹

------------------------------------------------------------

¹⁹ Das gilt auch für die folgenden Beispiele in 7.1.3, 7.1.4, 7.1.5.
²⁰ Hier wird zunächst aus Gründen der Transparenz ein vereinfachter Fall dargestellt: näich daß die Einzelstimmen nicht die Zeilen wechseln, also ohne Stimmkreuzungen gesetzt sind.
²¹ Vgl. Abschnitt 3.2

© 2000, zuletzt geändert am 11. Februar 2000.