A nonlinear model of the peripheral auditory system

Institute of Electronic Music, Jakoministrasse 3-5, A-8010 Graz, Austria
Dept. of Communications and Wave Propagation, Inffeldgasse 12, A-8010 Graz, Austria

Abstract

A nonlinear model of the peripheral auditory system is proposed. The spectral analysis is performed by a bank of overlapping bandpass filters. These auditory filters provide a functional representation of the operation performed by the inner ear. The model can be used as a preprocessor for e.g. speech recognition systems, loudness models or the evaluation of audio coding systems.

1. Introduction

The proposed nonlinear model of the peripheral auditory system consists of two main stages: outer-middle ear filtering and spectral analysis. The magnitude response of the outer-middle ear filter is estimated from the equal loudness contours [1]. To account for the fact that these contours are a matter of some controversy, the outer-middle ear filter is parameterized and can be easily adapted to any recent re-examinations.
The spectral analysis is calculated with a bank of overlapping bandpass filters. These so-called 'auditory filters' provide a functional representation of the operation performed by the inner ear. The excitation pattern of a given sound can be thought of as the output power of these auditory filters as a function of their center frequency [2]. This concept corresponds to the 'critical bandwidth' [3].

The most popular method for estimating the shapes of auditory filters is the notched-noise method. This method is based on the assumptions of the power spectrum model of masking [4]. To approximate the auditory filters, Patterson [5] suggested a family of simple functions called roex' (rounded exponentials). The simplest of these expressions is called the roex(p) filter shape:

The parameter p determines the bandwidth and the slopes of the skirts. For asymmetric filters, the parameter p has different values for the lower (p_l) and upper (p_u) branches.

Glasberg and Moore [6] proposed the parameters p_l and p_u as follows:

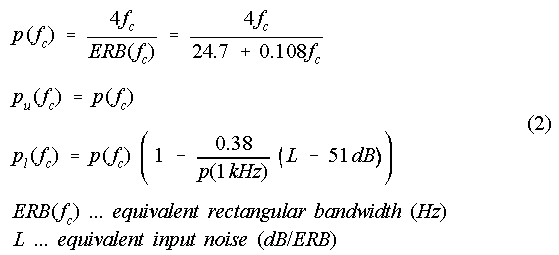
These auditory filters are approximately symmetric on a linear frequency scale when the input levels of the filters are equivalent to a level of L = 51 dB/ERB at 1 kHz (p_l(f_c) = p_u(f_c) = p(f_c). The low-frequency skirts of these auditory filters rise with increasing levels (L > 51 dB/ERB) and become steeper with decreasing levels (L < 51 dB/ERB). The upper-frequency skirts are level independent (cf. Figure 1).

A gammatone filter is described by its impulse response, which is called the gammatone function g(t):

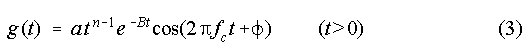
The parameter B mainly determines the bandwidth of the filter. The order n mainly determines the slope of the skirts. The center frequency of the filter is f_c [7]. The magnitude responses of gammatone filters (GTF) with order 4 are similar to the auditory filters given in Eq. (1) and (2) for L = 51 dB/ERB.
The gammatone function is similar to impulse responses obtained from cat experiments using the revcor technique [8]. For that reason, the gammatone filter can be considered as a link between physiological and psychoacoustic data. Detailed descriptions of the motivation for the gammatone filter are summarized in: [7], [9], [10], [11] and [12].

Linear (level-independent) GTF banks are appropriate for simulating the cochlear (inner ear) filtering of broadband sounds. Examples of linear filter banks are [13], [14] [15]. For narrowband sounds, the details of the filter shapes become more important because the slopes of the filters dominate the excitation pattern. Examples of level-dependent GTF banks are given in [12] (Parametrization of analog GTF), [16] (DRNL ... Dual Resonance Nonlinear Filter Model) and [17] (gammachirp function).

The presented level-dependent parameterization of All-Pole (APGTF) and One-Zero (OZGTF) gammatone filters is derived from Slaney's implementation [18] of a cochlear model proposed by Patterson [19]. To encompass the entire hearing range and to take into account common audio standards, the sampling rate is set to f_s = 44,1 kHz.

2. Outer-middle ear filtering

The model is designed to simulate monaural listening under free field conditions. Above 1kHz, the magnitude response of the outer-middle ear filter is similar to the inverted absolute threshold curve. This is based on the assumption that the inner ear is equally sensitive to all frequencies above 1 kHz. The absolute threshold curve is probably influenced by the low frequency internal noise of the inner ear and therefore does not reflect the transmission through the outer and middle ear below 1 kHz. We assume that the transmission through the outer and middle ear below 1kHz is reflected in the inverted shape of an equal-loudness contour at a high loudness level [1].
Several authors have found considerable deviations from the equal-loudness level contours described in ISO 226 [20]. These results led us to develop a modified phon-contour at a loudness level of 100 phon. This modification is an approximation of recent re-eximinations [21]. The outer-middle ear filter is parameterized and can be adapted to any recent re-examinations easily.

The transfer function of the outer-middle ear filter (H_OM(z) = H_LP(z) H_HP(z), Figure 2) consists of a cascade of a recursive lowpass filter of order 8

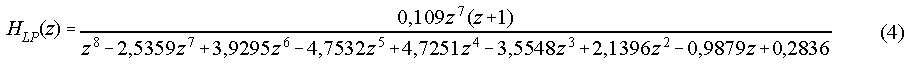
and a parameterized recursive highpass filter of order 2

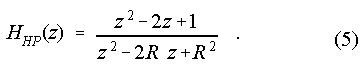
Possible magnitude responses for various values of the parameter R are shown in Figure 3.

Apart from the simple adaption to recent phon-contours, the internal noise of the inner ear (difference between outer-middle ear magnitude response and inverted absolute threshold, Figure 4) can be calculated straight forward. The frequency response of the parameterized highpass filter (Eq. (5)) is written in terms of a graphical evaluation (Figure 5).

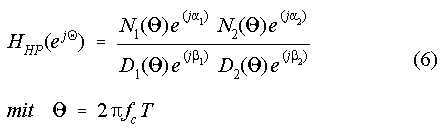
The two poles and two zeros are identical (N = N₁ = N₂, a = a₁ = a₂, D = D₁ = D₂, b = b₁ = b₂). The magnitude response becomes:

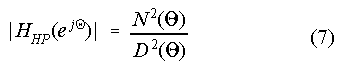
With D² = 1 + R² - 2Rcos(Q) (cf. Figure 5) the difference A_Diff between the outer-middle ear filter (R = R_OM) and the inverted absolute threshold contour (R = R_AT) becomes:

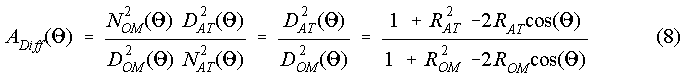
We are using an outer-middle ear filter with R_OM = 0.989 and we assume the inverted absolute threshold contour with R_AT = 0.957 at the moment.

3. Spectral analysis

The implementation of the nonlinear auditory filters is derived from an 8th order linear gammatone filter consisting of 4 biquad sections with 4 identical complex conjugate pole pair positions [18]:

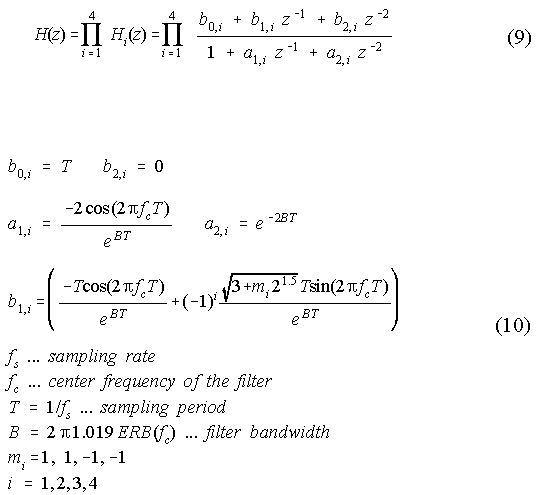
This linear gammatone filter becomes a nonlinear filter by moving the pole locations in the transfer functions H₂(z) - H₄(z) as a function of the control level L (Figure 6). Two different nonlinear filters are investigated, all- pole and one-zero gammatone filters. The difference between an all-pole and a one-zero gammatone filter is that a one-zero gammatone filter has one zero at z = 1 and an all-pole gammatone filter is a pure resonance filter. Since the first stage (H₁(z), cf. Figure 6) is level-independent, its output x₁(n) can be used to calculate the equivalent input noise level L. In the case of this input-level dependent control, a separate filter bank can be avoided.

The complex conjugate pole position of a single linear filter section is (cf. Eq. (10)):

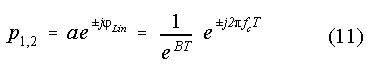
In the level-dependent displacement, the radius of the poles is held constant (a = const.). As a result, only the parameters a_1,i of the transfer functions H₂(z) - H₄(z) must be modified. The distance between the poles and the unit circle becomes larger with increasing pole-angles j_Lin = ±2pf_cT and the transfer function's sensitivity to pole-angle shifts decreases. Therefore the pole-angle shift should increase proportionally to j_Lin.

To obtain the proper pole-angle shift, j_Lin is multiplied by a level-dependent factor K:

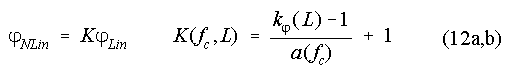
The factor K is obtained from the level-dependent parameter k_j and the radius a of the corresponding pole (Eq. (12b)). This equation causes an additional shift of the pole-angle at very high frequencies (f_c >> 1 kHz with f_s = 44,1 kHz). a ~ 1 results in K ~ k_j.
Combining Eq. (11) and (12a,b) the pole positions of the nonlinear filter sections become:

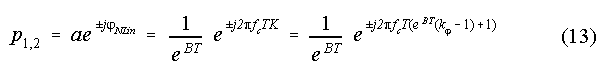
The level dependence of the parameter k_j is approximated with arctan-functions (Eq. (14) and (15), the indices 1,2,3,4 refer to the four filter sections).

(14)

• k_j for nlAPGTF:
  k_j1(L) = 1
  k_j2(L) = 0,9898 - 0,0066arctan(0,6(L-85))
  k_j3(L) = 0,893 - 0,075arctan(0,1(L-70))
  k_j4(L) = 1.0749 + 0,0165arctan(0,4(L-55))

(15)

• k_j for nlOZGTF:
  k_j1(L) = 1
  k_j2(L) = 0,9789 - 0,014arctan(0,2(L-80))
  k_j3(L) = 0,8673 - 0,093arctan(0,1(L-70))
  k_j4(L) = 1,0606 + 0,025arctan(0,1(L-68))

The parameter k_j is independent of the filter center frequency. It can be implemented with a single look-up table for all center frequencies respectively. For low control levels L, the pole locations are approximately the same as for the linear gammatone filters (cf. Eq. (10)).

The connection between the pole-shifts and the coefficients of the denominator (Eq. (9)) is shown in Eq. (16) and (17). The coefficients a_2,i are level-independent:

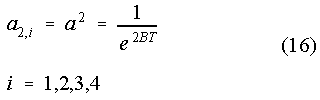
The coefficients a_1,i contain the level-dependent parameters k_j,i:

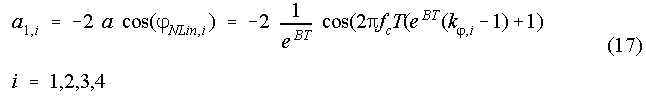
The coefficients of the numerator are:

(18)
nlAPGTF:
b_0,i=1, b_1,i=0, b_2,i=0
i = 1,2,3,4

(19)
nlOZGTF:
b_0,1=1, b_1,1=-1, b_2,1=0
b_0,i=1, b_1,i=0, b_2,i=0, i = 2,3,4

The sampling period T as part of the numerator of Eq. (10) does not appear in Eq. (18) and (19), because it is included in the amplification factors given in Eq. (20) and (21).
The magnitude of the first filter section H₁(z) has to be normalized to 0 dB at f_c, because its output x₁(n) might be used for the determination of the control level L. This gain normalization is achieved with the amplification factor V₁. Since the maximum of the magnitude response of the first section is at f_c (the pole-positions of the first section are never moved), V₁ can be derived directly from the transfer function H₁(z):

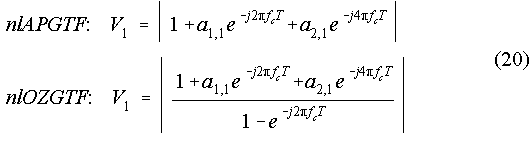
In contrast to H₁(z), the filter sections 2,3,4 cannot be separately normalized to 0 dB at f_c, because the maxima of the magnitude responses are moved with the pole-shifts. Therefore, an amplification factor V_com (Eq. (21)) is obtained from the combined transfer function H_com(z) = H₂(z) * H₃(z) * H₄(z). V₁ and V_com normalize the entire filter cascade to 0 dB at f_c.

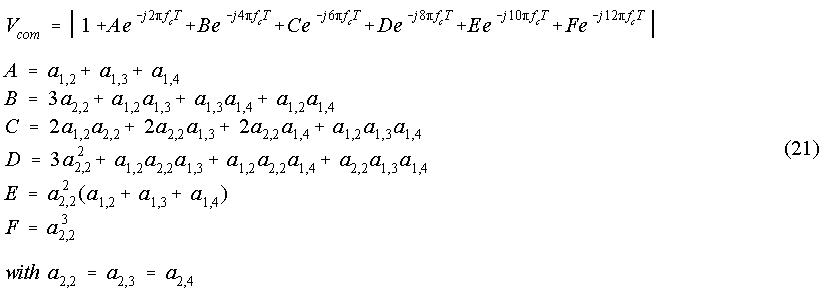
V_com can be used for both filter types because the transfer functions H₂(z) - H₄(z) are identical for nlAPGTF and nlOZGTF.

Using the transposed direct-form II, the implementation of the nonlinear filters is shown in Figure 7. The control unit for this implementation is shown in Figure 8. For comparison, the magnitude responses of the nlAPGTF and nlOZGTF are shown in Figure 9 and 10. Due to the 'missing' zero at z = 1, the low-frequency branch of the nlAPGTF results in a horizontal line the longer the distance to the center frequency is. For the nlOZGTF, this effect does not exist.

Assuming that the input signal of the nonlinear filter determines the slope of the low-frequency branch, the output of the first filter section x₁(n) can be used to calculate the control level L. Magnitude responses of the first filter section H₁(z) are plotted in Figure 11 with f_c = 100, 300, 1k, 3k, 10k Hz. These magnitude responses are independent of the control level.

4. Conclusion

The proposed model of the peripheral auditory system offers a basic concept for a level-dependent calculation of the time-frequency analysis performed in the inner ear. The model has been designed to simulate the frequency and time resolution. It is a prototype and not a complete application.
The magnitude response of the outer-middle ear filter is derived from equal loudness contours. The exact form of these countours is not clear at the moment. For that reason, the magnitude response of the outer-middle ear filter is parameterized and can be easily modified according to recent re-examinations of the phon-contours. The nonlinear gammatone filters (All-Pole and One-Zero filters) are derived from an 8th order linear gammatone filter [18]. The order of the nonlinear filters is fixed, which simplifies their implementation. The level dependent parameterization is given in a general form to adapt these filters to output level and input level dependent filter shapes.
To rise the low frequency branch, two complex conjugate pole pair locations are modified by decreasing the pole-angle. One pole pair location is changed by increasing the pole-angle to keep the filter center frequency constant. The radii of the pole pairs were held constant. A pole-angle shift larger than suggested is not useful, because the resonance frequencies of these poles would appear in the magnitude response as a ripple.
The group delay time at the resonance frequency decreases with increasing control levels. This corresponds to the auditory system because high-level signals are perceived earlier than low-level signals. Nevertheless this effect is too small to model psychoacoustic data.
To avoid transient responses in the filter output y(n) due to changes of the coefficients, the control level must be changed continuously. The output of the first filter section x₁(n) can be used to determine the control level for an input-level dependent control because H₁(z) is not affected by the parameterization. This would be very efficient because an additional signal path is avoided. Using a dynamic compression/expansion within the calculation of the control level, different control levels can be assigned to the shown magnitude responses.

Acknowledgements

This work was funded by the Austrian Science Foundation (FWF, project number: P11159-TEC).

References

[1] Moore B.C.J. and Glasberg B.R., 'A Revision of Zwicker's Loudness Model', Acustica - acta acustica, Vol. 82, 1996, 335-345
[2] Moore B.C.J., 'Characterisation of Simultaneous, Forward and Backward Masking', The Proceedings of the AES 12th International Conference - The Perception of Reproduced Sound, June 28-30, 1993, 22-33
[3] Zwicker E. , 'Psychoakustik', Springer Verlag, Berlin, Heidelberg, 1982
[4] Patterson R.D., Moore B.C.J.: 'Auditory Filters and excitation patterns as representations of frequency resolution', In: Moore B.C.J. (Ed.), Frequency Selectivity in Hearing, Academic, London, 1986, 123-177
[5] Patterson R.D., Nimmo-Smith I., Weber D.L., Milroy R.: 'The deterioration of hearing with age: Frequency selectivity, the critical ratio , the audiogram, and speech threshold', J. Acoust. Soc. Am. 72 (6), 1982, 1788-1803
[6] Glasberg B.R., Moore B.C.J.: 'Derivation of auditory filter shapes from notched-noise data', Hear. Res. 47, 1990, 103-138
[7] Patterson R.D.: 'The sound of a sinusoid: Spectral models', J. Acoust. Soc. Am. 96 (3), 1994, 1409-1418
[8] Carney L.H., Yin C.T.: 'Temporal coding of resonances by low-frequency auditory nerve fibres: single fibre responses and a population model', J. Neurophysiology, 60, 1988, 1653-1677
[9] Patterson R.D., Nimmo-Smith I., Holdsworth J., Rice P.: 'An efficient auditory filterbank based on the gammatone function', meeting of the IOC Speech Group on Auditory Modelling at RSRE, 1987
[10] Patterson R.D., Holdsworth J.: 'A functional model of neural activity patterns and auditory images', In Advances in Speech, Hearing and Language Processing, (W.A. Ainsworth, ed.) Vol 3. JAI Press, London
[11] Cooke M.: 'Modelling Auditory Processing and Organisation', Dissertation, University Sheffield, 1991, Cambridge University Press, 1993
[12] Lyon R.F.: 'The All-Pole Gammatone Filter and Auditory Models', Internet, temporäre Unterlagen für Computational Models of Signal Processing in the Auditory System', Forum Acusticum 1996, Antwerpen
[13] Patterson R.D., Allerhand M.H., Giguere C.: 'Time-domain modeling of peripheral auditory processing: A modular architecture and a software platform', J. Acoust. Soc. Am. 98 (4), 1995, 1890-1894
[14] Slaney M., Naar D., Lyon R.F.: 'Auditory model inversion for sound separation', Proc. of IEEE ICASSP, Vol. II, 1994, 77-80
[15] Meddis R.: LUTEar homepage', Internet WWW: ftp://suna.lut.ac.uk/public/hulpo/lutear/www/linklutear1.html
[16] Meddis R.: Dual resonance nonlinear filter (DRNL)', Internet WWW: http://info.lut.ac.uk/departments/hu/groups/speechlab/drnlpage.html
[17] Irino T.: A Gammachirp Function as an Optimal Auditory Filter with the Mellin Transform', IEEE ICASSP96, Atlanta, 1996, 981-984
[18] Slaney M.: An Efficient Implementation of the Patterson-Holdsworth Auditory Filter Bank', Apple Computer Technical Report #35, Apple Computer Inc., 1993
[19] Patterson R.D., Robinson K., Holdsworth J., McKeown D., Zhang C., Allerhand M.H.: Complex sounds and auditory images', In Auditory Physiology and Perception, (Eds.) Cazals Y., Demany L., Horner K., Pergamon, Oxford, 1992, 429-446
[20] Acoustics - Normal Equal-Loudness Level Contours', In ISO 226 (E), 1987, 20-27
[21] Suzuki Y., Sone T.: Frequency Characteristics of Loudness Perception: Principles and Applications', In Sixth Oldenburg Symposium on Psychological Acoustics, 1993, 193-221
[22] Fastl H., Jaroszewski A., Schorer E., Zwicker E.: Equal Loudness Contours between 100 and 1000 Hz for 30, 50, and 70 phon', Acustica Vol. 70, 1990, 197-201

© 2000 zuletzt geändert am 26. Jänner 2000.