Modellierung von HRTF - Kurven
Ziel der Modellierung ist eine möglichst recheneffiziente Nachbildung der HRTFs, um bei bestehender Rechenleistung möglichst viele Quellen spatialisieren zu können. Ein zusätzliches Problem stellt die Interpolation der HRTFs bei bewegten Quellen dar, da die perzeptiven Merkmale und nicht die einzelnen Abtastwerte interpoliert werden sollen.
Anwendung findet diese Technik z. B. in der virtuellen Akustik, wo Monoaufnahmen "verräumlicht" werden sollen. Eine andere Anwendung stellt der Versuch dar, aus mehrkanaligen Aufnahmen realer Schallsituationen ein Stereosignal für binaurale Wiedergabe zu berechnen.
1. Hauptkomponentenmethoden
1.1 AllgemeinesIm folgenden werden die verschiedenen Hauptkomponentenmethoden aus der Literatur behandelt. Es handelt sich dabei um dieselbe zugrundeliegende Idee, die verschiedenen Autoren verwenden dabei aber verschiedene Ausgangsmaterialien und Bezeichnungen.
1.2 Prinzip
Das Ausgangsmaterial stellt ein Satz von Außenohrkurven im Zeit- (HRIRs) oder Frequenzbereich (HRTFs) dar. Dieser Satz enthält Messungen aus n Richtungen zu je p Meßwerten. Daraus wird ein Set von Basisvektoren extrahiert, deren gewichtete Linearkombination die modellierten HRIRs bzw. HRTFs ergeben. Die richtungsabhängigen Gewichte repräsentieren den relativen Anteil jedes Basisvektors an einer Impulsantwort bzw. in einem Spektrum. Diese Art der Zerlegung bedeutet, daß Richtungskomponenten (in Form der Gewichte) und Frequenzkomponenten (in Form der Basisvektoren) getrennt werden.
Zuerst wird aus dem Satz von Außenohrkurven der Mittelwert gebildet:
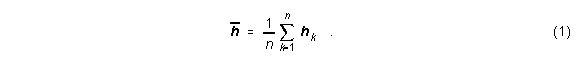
hk stellt die k-te HRIR bzw. HRTF dar. Die Bedeutung des Mittelwerts hängt von den verwendeten Daten ab. Im Fall von HRIRs oder "echten" HRTFs (reell oder komplex in
linearem Maßstab) enthält der gemittelte Vektor ![]() die subjektabhängigen und
richtungsunabhängigen spektralen Eigenschaften, die alle HRIRs bzw. HRTFs eines
individuellen Ohrs gemeinsam haben (z. B. die Ohrkanalresonanz um 2,5 kHz), sowie
Meßartefakte (z. B. spektrale Einbrüche durch stehende Wellen). Falls HRTFs in Form von
logarithmierten Amplitudengängen verwendet werden, stellt
die subjektabhängigen und
richtungsunabhängigen spektralen Eigenschaften, die alle HRIRs bzw. HRTFs eines
individuellen Ohrs gemeinsam haben (z. B. die Ohrkanalresonanz um 2,5 kHz), sowie
Meßartefakte (z. B. spektrale Einbrüche durch stehende Wellen). Falls HRTFs in Form von
logarithmierten Amplitudengängen verwendet werden, stellt![]() das geometrische Mittel
aus den linearen Amplitudengängen dar.
das geometrische Mittel
aus den linearen Amplitudengängen dar.
Die gemittelte Funktion![]() wird von den einzelnen HRIRs bzw. HRTFs subtrahiert. Durch
Entfernung des Mittelwerts enthalten die Ergebnisfunktionen dk primär richtungsabhängige
spektrale Effekte. Im Frequenzbereich nennt man die dk Richtungsübertragungsfunktionen
(directional transfer functions, DTFs), um sie von den HRTFs zu unterscheiden, im Zeitbereich
seien sie Richtungsimpulsantworten (directional impulse responses, DIRs) genannt.
wird von den einzelnen HRIRs bzw. HRTFs subtrahiert. Durch
Entfernung des Mittelwerts enthalten die Ergebnisfunktionen dk primär richtungsabhängige
spektrale Effekte. Im Frequenzbereich nennt man die dk Richtungsübertragungsfunktionen
(directional transfer functions, DTFs), um sie von den HRTFs zu unterscheiden, im Zeitbereich
seien sie Richtungsimpulsantworten (directional impulse responses, DIRs) genannt.
Die Wahl des Datenformats (HRIR, lineare HRTF oder logarithmierter Amplitudengang) wirkt sich auch auf die Filterstruktur für die Spatialisation aus. Um das Ausgangssignal o für die Richtung (Qk,jk) zu erhalten, wird das Audio-Eingangssignal s mit hk gefiltert. Es gilt:
![]()
Im Fall von HRIRs oder linearen HRTFs ergibt das Hinzufügen des Mittelwerts die Überlagerung der Ausgangssignale von zwei Filtern, bei logarithmierten HRTF-Amplitudengängen entspricht das aber einer Filterkaskade.
Für die DIRs bzw. DTFs wird die Kovarianzmatrix berechnet. Die Kovarianzen liefern ein Maß für die Ähnlichkeit zwischen zwei DIRs bzw. DTFs. Sei D eine p×n-Matrix, deren Spalten jeweils die DIR bzw. DTF einer bestimmten Richtung enthalten, dann berechnet sich die p×p-Kovarianzmatrix S folgendermaßen:
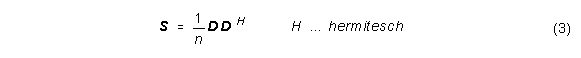
wobei n die Anzahl der gemessenen Richtungen ist.
Seien ci die Eigenvektoren von S und li die korrespondierenden Eigenwerte. Nachdem jede Autokorrelationsmatrix symmetrisch und nichtnegativ definit ist, gibt es p orthogonale Eigenvektoren, und die korrespondierenden Eigenwerte sind reell und nichtnegativ. Ohne Beschränkung der Allgemeinheit wählt man die Indizierung so, daß
![]()
Als Basisvektoren nimmt man die q Eigenvektoren von S, die mit den q größten Eigenwerten korrespondieren. Sie stellen die Spalten der orthonormalen Transformationsmatrix C dar:
![]()
Ist dk der k-te DIR- bzw. DTF-Vektor mit Dimension p×1, so ergeben sich die zugehörigen Gewichte wk folgendermaßen:
![]()
wobei C eine p×q-Matrix ist und wk der Gewichtsvektor mit Dimension q×1. Letzterer repräsentiert den Anteil der Basisvektoren an einer bestimmten dk.
CT transformiert also dk in einen Vektor wk, dessen Komponenten paarweise unkorreliert sind.
Diese spezielle Art der Orthogonaltransformation nennt man zeitdiskrete Karhunen-Loève
Transformation oder Hotelling Transformation (KLT).
Wenn q=p ist, dann erfüllt die reell- bzw. komplexwertige Matrix T=CT die
Orthogonalitätsbedingung
![]()
Eigenschaften einer Orthogonaltransformation sind:
- Die Distanz zwischen zwei beliebigen Punkten bleibt erhalten.
- Die Länge eines beliebigen Vektors bleibt erhalten.
- Die Determinante der Autokorrelationsmatrix des Eingangsvektors wird nicht verändert.
- Die Eliminierung der Korrelation zwischen den Transformationskoeffizienten reduziert das Produkt der Varianzen der Vektorkomponenten.
Die Autokorrelationsmatrix von wk ist gegeben durch
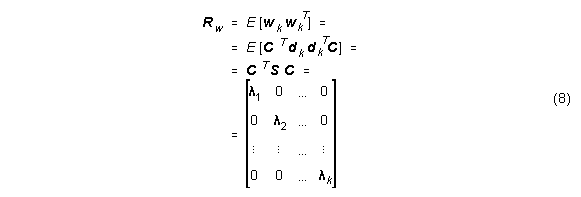
Man sieht, daß der Eingangsvektor tatsächlich dekorreliert wird.
Nach Umformung ergibt sich dk als gewichtete Summe der Basisvektoren:
![]()
Das Gleichheitszeichen gilt nur für q=p. In der Praxis ist qp, sodaß die rechte Seite obiger Gleichung nur eine Näherung für dk darstellt.
Je größer die Anzahl der Basisvektoren, desto besser die Näherung.
Um das Ausgangssignal o für die Richtung (Qk,jk) zu erhalten, wird das Audiodaten-Eingangssignal s mit dk gefiltert. Für HRIRs und lineare HRTFs gilt:
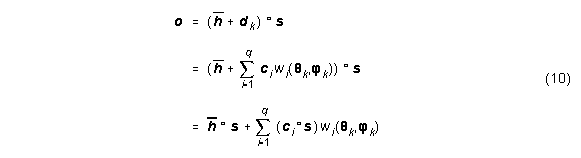
Für logarithmierte HRTFs gilt mit
![]()
die modifizierte Gleichung:
![]()
Nachdem ci nur frequenz- und nicht richtungsabhängig ist, kann bei bekannten Audiodaten die Filterung mit ci im voraus berechnet werden.
Die KLT minimiert den mittleren quadratischen Fehler für eine gegebene Zahl an Basisvektoren. Fünf Basisvektoren repräsentieren rund 90% der Varianz der menschlichen HRTF-Amplitude.
1.3 Hauptkomponentenanalyse und minimalphasige Rekonstruktion
Bei der Hauptkomponentenanalyse (principal components analysis, PCA) nach [Kistler, Wightman, 1995] und [Middlebrooks, Green, 1992] wird als Ausgangsmaterial der logarithmierte HRTF-Amplitudengang genommen. Die HRTF-Phase wird unter Annahme von Minimalphasigkeit und konstanter interauraler Phasen-(Zeit-)Differenz rekonstruiert. Letzteres bedeutet, daß nur eine einfache (konstante) Zeitverzögerung zur Berücksichtigung der ITD der jeweiligen Quellposition nötig ist.
Für die Berechnung der Richtungsübertragungsfunktionen (DTFs) werden alle (hier: 256) logarithmierten Amplitudengänge der HRTFs eines Ohres einer Person gemittelt.
Abbildung 1 zeigt die ersten fünf Basisfunktionen/-vektoren, Abbildung 2 zeigt für eine Richtung die gemessene HRTF (durchgezogene Linien) sowie die Ergebnisse der Rekonstruktion mit 1, 3 und 5 Basisvektoren (punktierte Linien).
Bezüglich der Körpergröße der Testpersonen konnte beobachtet werden, daß bei kleinen Personen die ersten 5 Basisfunktionen im Vergleich zu denen von großen Personen auf der Frequenzachse nach oben verschoben werden, wobei die Einhüllenden ähnlich sind.
1.4 Extraktion der spatialen Eigenschaften und Regularisierung
Dieser Abschnitt folgt [Chen et al., 1995], [Marolt, 1996] sowie [Gersho, Gray, 1992]. Die Basisfunktionen ci werden hier Eigenübertragungsfunktionen (eigentransfer functions, EFs), die Gewichte wi(Qk,jk) "spatial-charakteristische" Funktionen (spatial charactaristic functions, SCFs) genannt. Das Ausgangsmaterial bilden die komplexwertigen HRTFs (Amplitude und Phase).
Das Modell für die Nachbildung der HRTFs im Frequenzbereich, hm(Qk,jk), ist ein p×1 Vektor und lautet:
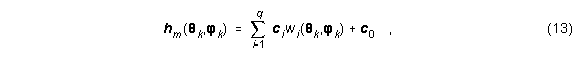
wobei (Qk,jk) die Richtung der virtuellen Quelle, hm(Qk,jk) die modellierte HRTF, ci (i = 0,...,q) die Eigenübertragungsfunktion und wi(Qk,jk) die spatial-charakteristische Funktion ist.
Der mittlere quadratische Fehler ek einer bestimmten Richtung (in Abb. 3 und 4 als "Error" angegeben) ist definiert als
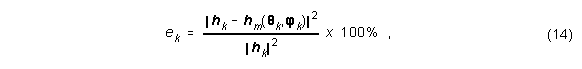
wobei hk die k-te gemessene HRTF und hm(Qk,jk) durch Gleichung (13) gegeben ist. Der gesamte mittlere quadratische Fehler e (Abb. 5) sinkt mit der Anzahl q der EFs und ist definiert als
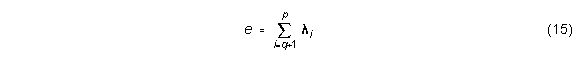
Abbildung 6 zeigt die gemittelte HRTF sowie die ersten sieben EFs für KEMAR.
In Abbildung 3 sind nur Richtungen abgebildet, die zur Bestimmung der Modellparameter verwendet worden sind. Man sieht, daß die Fehler der interpoliert modellierten HRTFs aus Abbildung 4 etwas größer sind als die aus Abbildung 3.
1.5 Extraktion der spatialen Eigenschaften im Zeitbereich
Bei [Wu et al., 1997] stellen normalisierte Außenohrimpulsantworten (head-related impulse responses, HRIRs) das Ausgangsmaterial dar.
Die Gewichte wi(Q,j) werden als reelle spatial-charakteristische Funktionen (real spatial characteristic functions, RSCFs) bezeichnet und sind reellwertige Funktionen des räumlichen Ortes. Die normalisierten HRIRs werden im kontinuierlichen Raum (Q,j) als
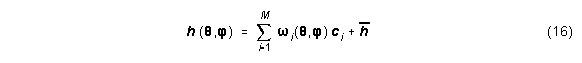
repräsentiert.
Abbildung 7 zeigt die gemittelte HRIR und die ersten sechs Basisfunktionen für die HRIRs einer Katze.
Schätzungen für beliebige Richtungen erhält man, indem man die RSCFs, ITDs und IIDs der gemessenen Richtungen interpoliert. Verwendet man den Interpolationsalgorithmus für den linearen Raum für eine Richtung (Q,j) mit Elevation -36°...+90°, so erhält man als Schätzwerte für die RSCFs
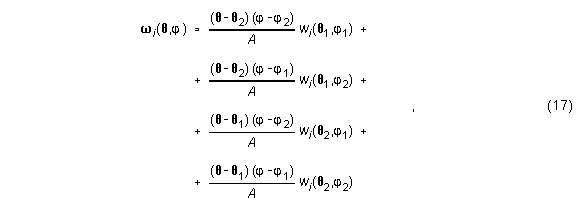
wobei hier A=9x9 eine Fläche auf einem 9°-Netz ist und (Q1,j1), (Q1,j2), (Q2,j1) und (Q2,j2) die vier benachbarten Meßpunkte von (Q,j) sind.
Die Abbildungen 8 und 9 zeigen Höhenliniendarstellungen der ITDs und IIDs.
2. FIR- und IIR-Filterdesign
Dieser Abschnitt folgt [Jot et al., 1995] und [Brandenstein, Unbehauen, 1998].Folgende Eigenschaften werden beim Design von Synthesefiltern genutzt:
- Lineare Filter können in ein minimalphasiges Filter und ein Allpaßfilter zerlegt werden ({magnitude, excess phase} Darstellung). Das Allpaßfilter realisiert eine "excess phase", die man erhält, wenn man von der Phasenantwort den minimalphasigen Anteil subtrahiert. Den minimalphasigen Phasengang erhält man durch Anwendung der Hilbert-Transformation auf den logarithmierten Amplitudengang.
- Bei HRTFs kann das Allpaßfilter als eine einfache Zeitverzögerung angenähert werden, dies gilt zumindest für den Bereich bis zu 10 kHz. In diesem Bereich ist die "excess phase" eine lineare Funktion der Frequenz. Diese Zeitverzögerung schätzt man durch eine Gerade ab, die durch die "excess phase"-Antwort im Bereich von 1 kHz bis 5 kHz gelegt wird.
2.1 FIR-Filterdesign
Experimente von D. J. Kistler und F. L. Wightman sowie D. Hammershøi und J. Sandvad konnten zeigen, daß eine minimalphasige Approximation von HRTFs die Lokalisationsgenauigkeit nicht beeinflußt.
Vorgangsweise:
- Repräsentation der HRTFs als {magnitude, excess phase} Darstellung.
- Näherung der excess phase als einfache Zeitverzögerung.
- Diffusfeld-Entzerrung des Amplitudengangs.
- Minimalphasige Rekonstruktion der FIR-Filterantwort unter Verwendung von Hilbert-Transformation und inverser Fourier-Transformation.
- HRTF-Approximation durch Kaskadierung der Zeitverzögerung und des minimalphasigen Filters.
2.2 IIR-Filterdesign
Vorgangsweise:
- Repräsentation der HRTFs als {magnitude, excess phase} Darstellung.
- Näherung der excess phase als einfache Zeitverzögerung.
- Diffusfeld-Entzerrung des Amplitudengangs.
- "Constant Q smoothing": Glätten des Amplitudenspektrums unter Verwendung eines Hann-Fensters mit frequenzproportionaler Breite.
- "Warping": Resampling des Amplitudenspektrums auf einer verzerrten ("warped") Frequenzskala entsprechend der Bilineartransformation z->(z+r)/(1+rz) mit r = -1...+1.
- Näherung des verzerrten Amplitudenspektrums mittels Yule-Walker-Algorithmus ergibt
die Übertragungsfunktion
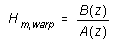 .
. - "Dewarping": Anwendung der Bilineartransformation z->(z-r)/(1-rz) auf die Übertragungsfunktion Hm, warp(z) ergibt Hm(z).
Die Frequenzverzerrung hat den Effekt des Oversampling bei niederen und Undersampling bei hohen Frequenzen, daher muß das Spektrum vorher geglättet werden. r kann so gewählt werden, daß die neue Frequenzachse in etwa der Barkskala entspricht. Der Verlust an Genauigkeit bei hohen Frequenzen wird für eine besserer Näherung bei tieferen Frequenzen in Kauf genommen.
Abbildung 10 zeigt die Ergebnisse der HRTF-Modellierung nach [Jot et al., 1995].
Eine alternative Designmethode wird in [Brandenstein, Unbehauen, 1998] angegeben. Dabei wird ein FIR-Filter durch ein IIR-Filter angenähert:
Gegeben sei die Übertragungsfunktion F(z) eines FIR-Filters mit
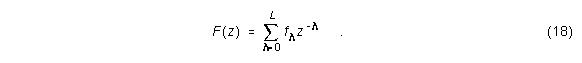
Diese soll durch ein IIR-Filter mit der Übertragungsfunktion H(z)
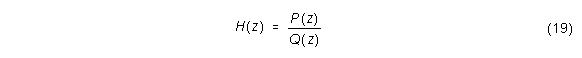
angenähert werden, wobei N<L sowie
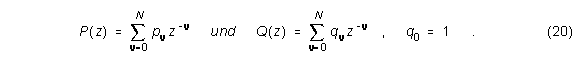
Das bedeutet, daß man N+1 reelle Zählerkoeffizienten p und N reelle Nennerkoeffizienten q bestimmen muß, sodaß die L2-Norm der Differenzfunktion D(z)
![]()
minimiert wird. Die L2-Norm von D(z) ist definiert als
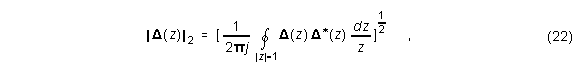
wobei die Integration gegen den Uhrzeigersinn durchgeführt werden muß und "*" für konjugiert-komplex steht. Nachdem das IIR-Filter stabil sein soll, müssen alle Pole von H(z) innerhalb des Einheitskreises (|z|<1) liegen und die Funktion H(z) außerhalb des Einheitskreises (|z|>1) analytisch sein.
Theorem von Walsh
Dieses Theorem wurde ursprünglich für die Näherung von Funktionen formuliert, die
analytisch in |z|<1 sind, es kann aber leicht für |z|>1 übertragen werden.
In der Menge der rationalen Funktionen H(z) [nach Gleichungen (19) und (20)] mit den Polen a1,...,aN innerhalb des Einheitskreises ist die beste Approximation für F(z) (analytisch in |z|>1 und kontinuierlich in |z|1) im Sinne der kleinsten quadratischen Fehler jene eindeutige Funktion, die F(z) in den Punkten z=,1/a1*,...,1/aN* interpoliert.
Dieses Theorem kann man verwenden, um die Bestimmung der Zählerkoeffizienten pv und der Pole av zu entkoppeln. Hat man die Pole bestimmt, ergeben sich die Zählerkoeffizienten als Lösung eines Interpolationsproblems. Es können immer N+1 lineare Gleichungen in N+1 Unbekannten pv für die Interpolation angegeben werden, was zu einer eindeutigen Lösung führt. Sind alle av verschieden, so ist dies offensichtlich. Definiert man
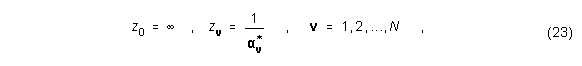
so lautet die Bedingung einfach
![]()
Nachdem alle Pole paarweise verschieden sind, erhält man N+1 linear unabhängige Gleichungen in N+1 Unbekannten pv.
Bei mehrfachen Polen oder mindestens einem Pol an der Stelle z=0 wird für die Aufstellung der Bestimmungsgleichungen die der Multiplizität des jeweiligen Pols entsprechende Anzahl von Ableitungen der Gleichung (24) nach z-1 an der Stelle des Pols verwendet.
2.3 Zeitvariante Implementation
Hier kann man zwei verschiedene Prozesse der zeitvarianten Implementation unterscheiden:
Interpolation:
Unter Interpolation versteht man die Synthetisierung einer Übertragungsfunktion unter
Verwendung einer Datenbank aus vordefinierten Filtern. In unserem Fall besteht die
Datenbank aus Richtungsfilterpaaren, die durch Näherung der gemessenen HRTF-Kurven
gewonnen worden sind.
Kommutation:
Kommutation bedeutet Update der Filterkoeffizienten, während das Filter "läuft". Der
Prozessor realisiert das Update sofort zwischen der Berechnung zweier aufeinanderfolgender
Output-Samples. Das Update von Koeffizienten in einem digitalen Filter kann hörbare Klicks
verursachen.
In einem synchronen Operationsmodus wird typischerweise in regelmäßigen Zeitintervallen die neue Zielposition angegeben. Das Update der Filterkoeffizienten kann durch folgende zyklische Prozedur vorgenommen werden:
- Lesen eines neuen Filterpaares entsprechend der neuen Richtung aus der Datenbank bzw. Berechnen eines neuen Filterpaares durch Interpolation.
- Initialisierung des Kommutationsprozesses: Berechnen der elementaren Inkremente für alle Koeffizienten, die die Kommutation kontrollieren.
- Inkrementieren und Updaten der Filterkoeffizientensets in regelmäßigen Zeitabständen, bis die nächste gewünschte Richtung erreicht ist. Danach zurück zu Punkt 1.
3. Modellierung durch Richtstrahlbildung
3.1 Allgemeines
Die Methode der Richtstrahlbildung (Beamforming) wird in [Chen et al., 1992] behandelt.
Am Ausgang eines Richtstrahlers (Beamformer) liegt eine gewichtete Kombination der Daten
an, die an einem Feld von räumlich verteilten Sensoren empfangen worden sind. Die
Gewichte des Richtstrahlers und die Sensor-Feldgeometrie determinieren die räumliche und
zeitliche Filtercharakteristik. Im vorliegenden Fall ergibt sich die Sensorgeometrie aus der
Außenohrakustik. Die Gewichte werden so gewählt, daß der mittlere quadratische Fehler
zwischen der Richtstrahler-Antwort und den gemessenen Außenohrantworten minimiert wird.
Die Modellantwort ist das innere Produkt aus dem Gewichtsvektor und einem
Feldantwortvektor (array response vector). Letzterer repräsentiert explizit die Feldgeometrie
und den Ort der Quelle.
Es handelt sich um eine Modellierung der Transformationseigenschaften des Außenohres als
Eingangs-Ausgangs-Beziehung.
Die Vorteile dieses Verfahrens sind:
- Es liefert einen expliziten mathematischen Ausdruck, der die Richtungsabhängigkeit der Schallwelle am Trommelfell enthält.
- Es repräsentiert die Außenohrübertragungscharakteristik als eine kontinuierliche Funktion der räumlichen Richtung, auch wenn die Modellparameter durch diskrete Messungen ermittelt wurden.
- Substantielle Datenkompression bei Repräsentation von HRTFs mit vielen Richtungen und Frequenzen.
3.2 Prinzip
Wie aus Abbildung 11 ersichtlich, enthält der Richtstrahler M Sensoren, wobei sich in jedem Sensorkanal ein FIR-Filter der Länge N+1 befindet. Die Antwort h(w,Q) des Richtstrahlers (= modellierte HRTF) wird durch den Feldantwortvektor d(w,Q) und den Gewichtsvektor wH dargestellt:
![]()
Dabei ist w die Kreisfrequenz und Q der Azimut sowie
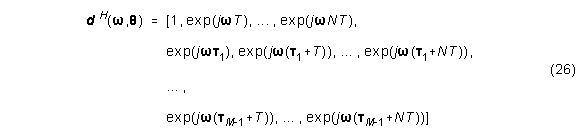
und
![]()
Dabei ist N+1 die FIR-Filterordnung, T das Abtastintervall (im folgenden sei der Einfachheit wegen T=1) und Ti die Zeitverzögerung zufolge Ausbreitung zwischen erstem und i-tem Sensor. Ti enthält die Sensorfeldgeometrie sowie die Richtung Q der Quelle. In Gleichung (27) bezieht sich das erste Subskript auf den Kanal-Index und das zweite auf den Tap-Index.
3.3 LMS-Richtstrahler Design
Ziel ist die Bestimmung von w für eine gegebene Feldgeometrie, sodaß der Richtstrahler eine gewünschte Antwort annähert. Eine Optimierung der Feldgeometrie wird nicht in Betracht gezogen, da dies ein schwieriges Problem ist aufgrund der komplizierten Art, mit der die Geometrie in d(w,Q) eingeht.
Wenn hd(w,Q) die gewünschte Antwort (hier: Außenohrantwort) darstellt, so beträgt der Fehler
![]()
Die Minimierung des mittleren quadratischen Fehlers bedeutet
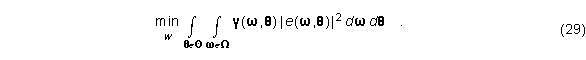
Dabei ist (w,Q) ein nicht-negative Gewichtsfunktion, um bestimmte Frequenzen und Richtungen hervorzuheben. Nachdem von den n HRTFs aus Richtung wi (i=1,...,n) nur je p diskrete Meßwerte bei den Frequenzen j (j=1,...,p) vorliegen, reduziert sich die Lösung auf
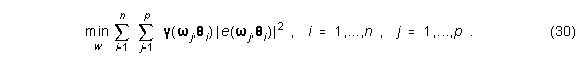
Der Fehlervektor eH ist definiert als:
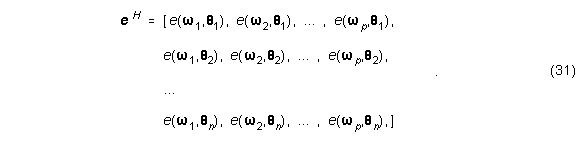
Sei
![]()
wobei
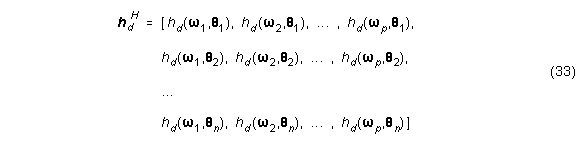
und
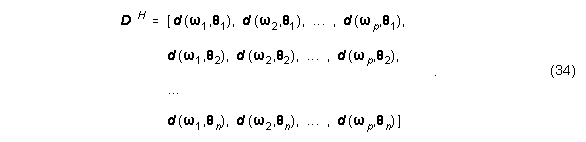
Nun schreibt man (wj,Qi) als diagonale Gewichtsmatrix der Dimension p×n um:
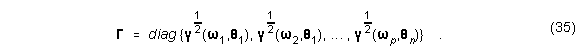
Gleichung (30) wird nun geschrieben als
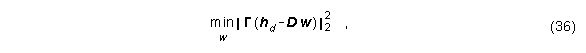
was äquivalent ist zu einer Lösung von S=p×n linearen Gleichungen in L=M×(N+1) Unbekannten
![]()
Im allgemeinen ist S>L.
Bisher wurde w komplex angenommen. Die Antwort der zu modellierenden physikalischen
Systeme ist aber konjugiert-komplex symmetrisch auf der Frequenzachse, das heißt
![]()
Nun sind
![]()
Nachdem d*(w,Q) = d(-w,Q), ist
![]()
Dies impliziert, daß wT = wH. Daher ist w reellwertig und es gilt:
![]()
wobei die Indizes I und R Imaginär- bzw. Realteil der jeweiligen Größe bezeichnen.
Die Euklidische Norm eines Vektors ist folgendermaßen definiert:
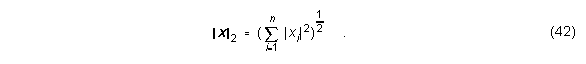
Nachdem
![]()
ist leicht zu zeigen, daß Gl. (36) äquivalent ist zum reellwertigen Problem

Zur Lösung dieser Gleichung kann man C mittels Singulärwertzerlegung (singular value decomposition, SVD) als Produkt seiner Singulärwerte und -vektoren darstellen:
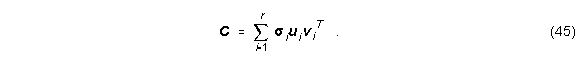
r ist der Rang von C, ui und vi sind die Links- bzw. Rechtssingulärvektoren und si die Singulärwerte. Unter der Annahme von s1³s2³...³sr³sr+1=...=sL=0 ergibt sich die Lösung von w als
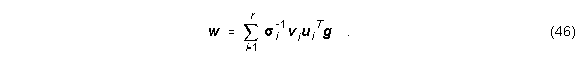
Ist die Matrix C "rank deficient", so ergibt eine numerische Auswertung der SVD Singulärwerte, die nicht exakt gleich Null sind. Diese sehr kleinen Singulärwerte bewirken eine sehr große Norm von w. Daher verwendet man meist nur r signifikante Singulärwerte, um w zu lösen:
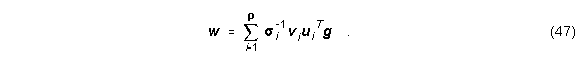
r wird entsprechend der Anzahl der Singulärwerte gewählt, die über einer bestimmte d Schwelle liegen. Der mittlere quadratische Fehler von Gl. (47) ist
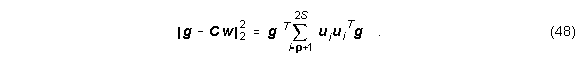
Die Norm von w ist
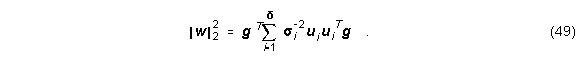
Mit sinkendem r steigt der Fehler und sinkt die Norm von w.
3.4 Beschreibung der experimentellen Daten
Das Modell wurde mit der Außenohrübertragungsfunktion einer Katze verifiziert. Diese hat einen größeren Frequenzbereich und eine ähnliche spektrale Einhüllende wie die eines Menschen.
Es gab drei Ansätze zur Phasenrekonstruktion:
- Linearphasen-Methode: Statt der originalen Phase wird eine lineare Phase mit einer Gruppenverzögerung proportional zum zeitlichen Öffnungszentrum (temporal aperture center) des Richtstrahlers verwendet.
- Minimalphasen-Methode: Die originale Phase wird durch ihre minimalphasige Komponente ersetzt. Dies garantiert eine eindeutige Darstellung der originalen Außenohrübertragungsfunktion mit minimaler Zeitverzögerung.
- Allphasen-Methode: Zerlegung des Originalphase in eine minimalphasige und eine Allpaß-Komponente. Die Allpaß-Komponente wird geglättet und daraus die lineare Komponente, die ehne reine Zeitverzögerung darstellt, entfernt. Die verbleibende nichtlineare Komponente wird zur minimalphasigen Komponente hinzuaddiert.
Die Linearphasen-Methode liefert für eine gegebene Feldstruktur die beste Näherung der gewünschte Amplitudenantwort, sie ignoriert jedoch die Phasenbeziehungen. Daher gibt es erhebliche Unterschiede zwischen der modellierten und der gemessenen Impulsantwort. Die Allphasen-Methode liefert im Vergleich zur gemessenen Impulsantwort die geringste morphologische Zerstörung der modellierten Impulsantwort. Sie ergab aber den größten Fehler zwischen modellierter und gemessener Frequenzantwort. Die Minimalphasen-Methode stellt einen Kompromiß zwischen den beiden Methoden dar.
3.5 Experimentelle Ergebnisse
Es werden sowohl verschiedene Feldstrukturen bezüglich des mittleren Näherungsfehlers
untersucht als auch der Interpolationsfehler und der Fehler im Zeitbereich.
Gute Ergebnisse lieferte eine 5-1-5 L-förmige Sensorgeometrie mit 8 mm Sensorabstand und
je 40...50 Filter-Taps.
Allerdings wurden nur verschiedene Außenohrkurven gleicher Elevation untersucht. Will man
die binaurale Außenohrantwort nachbilden, so muß man auf eine dreidimensionale
Feldgeometrie erweitern sowie die interauralen Zeitdifferenzen berücksichtigen.
Abbildung 12 zeigt den mittleren Näherungsfehler als Funktion der Anzahl der Sensoren und der FIR-Filterlänge. Der mittlere Näherungsfehler ist definiert als
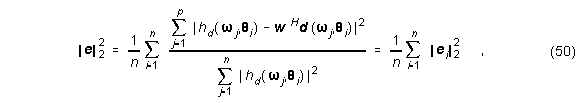
wobei
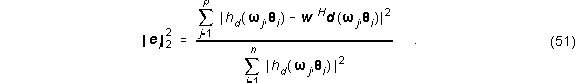
Abbildung 13 zeigt den Vergleich von gemessenen und modellierten Amplitudenantworten in 4 verschiedenen Richtungen für verschiedene Anzahl von Sensoren und FIR-Filterlängen.
Abbildung 14 zeigt den Näherungsfehler als Funktion der Anzahl von Sensoren an jeder Achse einer L-förmigen Feldgeometrie. Jeder Sensorkanal enthält ein FIR-Filter der Länge 64, der Abstand zwischen den Sensoren beträgt 8mm. Abbildung 15 zeigt den Näherungsfehler in Abhängigkeit von der Filterlänge in jedem Kanal eines 5-1-5 L-förmigen Feldgeometrie. Der Abstand der Sensoren beträgt jeweils 8 mm.
Abbildung 16 zeigt den mittleren Näherungsfehler in Abhängigkeit vom Abstand der Sensoren für sechs verschiedene Sensorkonfigurationen. Alle Konfigurationen haben FIR-Filter der Länge 64 in jedem Sensorkanal.
Balanced Model Truncation (BMT)
4.1 AllgemeinesEine balancierte Realisierung ist eine spezielle Zustandsraumdarstellung eines Systems mit bestimmten Eigenschaften, die es ermöglichen, durch Partitionierung die Ordnung des Systems zu reduzieren. Das ordnungsreduzierte System stellt dann eine Näherung für das Originalsystem dar. Definiert man in geeigneter Weise einen Näherungsfehler, so kann man für diesen eine obere Schranke angeben. Man nützt diese Erkenntnisse, um für ein gegebenes FIR-Filter eine spezielle Zustandstransformation so anzugeben, daß das System in eine balancierte Realisierung übergeführt wird und anschließend reduziert werden kann. (Die Methode der balancierten Realisierung basiert auf der Wahl der Zustandsvariablen.)
Diese Methode wird in [Mackenzie et al., 1997], [Beliczinski et al., 1992] und [Kale, 1993] behandelt.
In Abschnitt 4.5 werden weitere mathematische Zusammenhänge angeführt, auf die im Text mit "siehe Zusatz X in Abschnitt 4.5" verwiesen wird.
4.2 Prinzip der balancierten Realisierung und Modellreduktion
Zu einer Übertragungsfunktion F(z)
![]()
eines Übertragungssystems kann ein Zustandsraummodell der Form
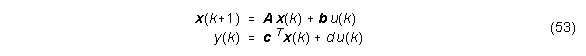
angegeben werden. Hierbei ist x der Zustandvektor, u die skalare Eingangsgröße und y die skalare Ausgangsgröße.
Zu einer Übertragungsfunktion gibt es bekanntlich unendlich viele Eingangs-/Ausgangs-äquivalente Realisierungen im Zustandsraum. Von einer Zustandsraumdarstellung gelangt
man mittels einer regulären Zustandstransformation ![]() in eine andere:
in eine andere:
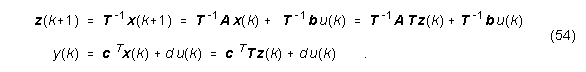
Somit sind
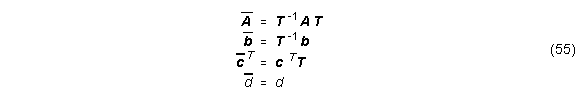
die entsprechenden Größen der Zustandsraumdarstellung des Modells in z.
Die zugehörige Übertragungsfunktion ändert sich nicht, d. h. es gilt:
![]()
Definition: Balancierte Realisierung
Einer Zustandsraumdarstellung des Systems (A, b, c) können zwei spezielle Matrizen P und
Q zugeordnet werden. Sie sind die Lösungen der Ljapunow-Gleichungen:
![]()
und
![]()
Diese Matrizen P und Q sind als Steuerbarkeits- bzw. Beobachtbarkeits-Gramsche Matrizen bekannt. Wenn das Übertragungssystem (A, b, c) asymptotisch stabil ist und das Paar (A, b) vollständig steuerbar und (A, c) vollständig beobachtbar ist, dann sind P und Q positiv-definite Matrizen. Diese sind dann eindeutig bestimmbar.
Eine Zustandsraumdarstellung mit der Eigenschaft, daß für die Matrizen P und Q gilt:
![]()
nennt man balancierte Realisierung (balanced realization).
Die Wahl der Transformation T, die zu einer balancierten Realisierung führt, wird in Zusatz 1 in Abschnitt 4.5 beschrieben.
Eigenschaften einer balancierten Realisierung
Wendet man eine Transformation T auf das System (A, b, c) an, so besitzt das neue System
![]() neue Gramsche Matrizen
neue Gramsche Matrizen ![]() und
und ![]() , die sich aus folgenden Gleichungen ergeben:
, die sich aus folgenden Gleichungen ergeben:
![]()
und
![]()
Setzt man nun Gleichung (55) in die Gleichungen (60) und (61) ein, dann erhält man
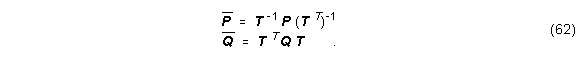
Die Gramschen Matrizen P und Q hängen stark von der Wahl der Zustandsgrößen ab. Die Eigenwerte ihres Produkts li (PQ) aber sind invariant unter einer Zustandstransformation und daher eine Eingangs-/Ausgangs-Invariante.
Sind alle Eigenwerte der Matrix A negativ, d. h. Re(li(A))<0, dann sind die Hankel-Singulärwerte (Hankel Singular Values, HSVs) von F(z) definiert als
![]()
Diese Werte sind üblicherweise in absteigender Reihenfolge geordnet:
![]()
Der maximale Singulärwert definiert die sogenannte Hankel-Norm einer Übertragungsfunktion:
![]()
Theorem: Balanced Model Truncation (BMT)
Ein balanciertes System (Ab, bb, cb) der Ordnung n kann im Zustandsraum in zwei
Untersysteme partitioniert werden, nämlich in ein gestutztes (truncated) System (A11, b1, c1)
der Ordnung k und ein verworfenes (rejected) System (A22, b2, c2) der Ordnung n-k:
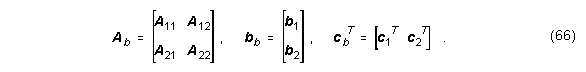
Die zum Übertragungssystem gehörigen Matrizen Pb und Qb (nach Gln. (57) und (58)) sind dann durch å folgendermaßen darstellbar:
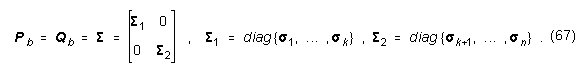
Ist das System (Ab, bb, cb) asymptotisch stabil, balanciert, vollständig steuerbar und vollständig beobachtbar, so ist das gestutzte Subsystem (A11, b1, c1) der Ordnung k ebenfalls asymptotisch stabil, balanciert, vollständig steuerbar und vollständig beobachtbar.
Fk(z) ist nun die Übertragungsfunktion, die man durch Stutzung (truncation) der balancierten Realisierung F(z) auf die ersten k Zustände erhält:
![]()
k kann beliebig gewählt werden. Eine wichtige Entscheidungsgrundlage bildet aber die folgende Eigenschaft:
Durch die in Gleichung (65) definierte Hankel-Norm kann eine Abschätzung für die reduzierte Übertragungsfunktion Fk(z) folgendermaßen angegeben werden(1):
![]()
Das heißt, die Hankel-Norm der Differenz zwischen der originalen Systemübertragungsfunktion F(z) und der angenäherten Fk(z) ist kleiner oder gleich der Summe der HSVs des verworfenen Systems. Wenn die HSVs des verworfenen Systems "viel kleiner" als die des gestutzten Systems sind, wird der Näherungsfehler klein. In der Praxis ist die Reduzierbarkeit der Ordnung des Systems von der Verteilung der HSVs der balancierten Form des Originalsystems abhängig.
Berechnung der Hankel-Singulärwerte und Bestimmung einer balancierten Realisierung
Die Hankel-Norm kann zur Berechnung der HSVs verwendet werden. Für das
Übertragungssystem (A, b, c) sind die Markow-Parameter Hk definiert als
![]()
Die Markow-Parameter repräsentieren die Impulsantwortfolge des Übertragungssystems (A,b,c). Die Hankel-Matrix H ist folgendermaßen definiert:
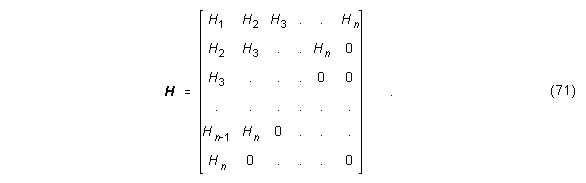
Die Hankel-Singulärwerte von F(z) sind die Eigenwerte von H und es gilt:
![]()
Weitere Zusammenhänge zwischen P, Q und H werden in Zusatz 2 in Abschnitt 4.5 angegeben.
Nachdem H eine symmetrische Matrix ist, kann sie wie folgt faktorisiert werden:
![]()
wobei
![]()
Dabei ist L eine Diagonalmatrix und I die Einheitsmatrix.
Ein Folgesatz betreffend P und Wc (siehe Zusatz 2) wird in Zusatz 3 in Abschnitt 4.5 angegeben.
Die Zustandstransformation
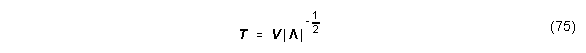
führt zu einer balancierten Realisierung des Systems, wobei |.| die absoluten Werte der Matrixelemente symbolisiert.(2). Weiters kann man zeigen, daß
![]()
Die Zusammenhänge zwischen H, P, Q, V und L werden in Zusatz 4 in Abschnitt 4.5 angeführt.
Verwendet man die Zustandstransformation aus Gleichung (75) unter Anwendung von Gleichung (62), so erhält man
![]()
Hat man diese balancierte Realisierung, so kann man die Ordnung des Systems reduzieren, indem man ein gestutztes System bildet.
Falls diese Realisierung aufgrund der stark variierenden Diagonalelemente von L nicht gut ist, kann man auch die folgende Transformation verwenden:
![]()
Man erhält dadurch das System in einer Form, die als "input normal" bezeichnet wird. Die Übertragungsfunktion, die man durch Transformation nach Gleichung (78) erhält, ist identisch zu jener, die sich durch Transformation nach Gleichung (75) ergibt.
Die wichtigen (und praktischen) Zusammenhänge zwischen dem System (Ak, bk, ck) bzw. (Ab, bb, cb) und V und L enthält Zusatz 5 in Abschnitt 4.5.
4.3 Konversionsalgorithmus FIR -> IIR
Gegeben sei ein FIR-Filter mit N Koeffizienten (ein System (N-1)-ter Ordnung, d. h. n=N-1), geschrieben in der folgenden Form als Übertragungsfunktion:
![]()
Das Filter F(z) kann (wie in Abschnitt 4.2 beschrieben) als Zustandsraummodell angegeben werden:
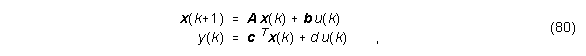
wobei
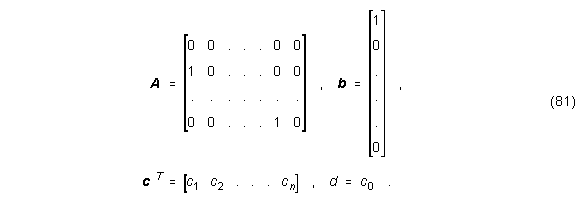 Zu bemerken ist, daß das Filter F1(z) allein durch A, b und c dargestellt werden kann.
Zu bemerken ist, daß das Filter F1(z) allein durch A, b und c dargestellt werden kann.
Da das System (A, b, c) eine endliche Impulsantwort besitzt, wird nun die finite Hankel-Matrix nach Gleichung (70) gebildet:
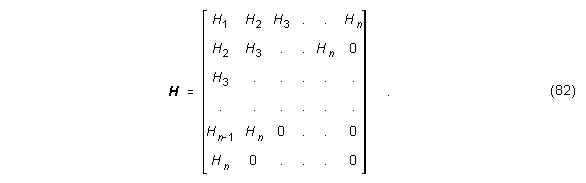
Danach wird mit H eine Singulärwertzerlegung (singular value decomposition, SVD) durchgeführt, als Ergebnis erhält man die HSVs.
Bei Darstellung der HSVs als Plot kann man sofort die voraussichtliche Ordnung k der Näherung ablesen: Sie entspricht der Anzahl der k größten HSVs, die im Vergleich zu den nachfolgenden nicht vernachlässigt werden können. Der zu erwartende Fehler kann mit Gleichung (69) abgeschätzt werden.
Danach erfolgt die Berechnung des gestutzten Systems:
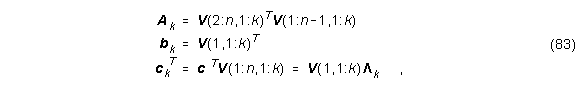
wobei V(i:j, k:m) die Extraktion der Reihen i bis j und der Spalten k bis m der Matrix V bedeutet.
Die Übertragungsfunktion Fr(z) des reduzierten Systems (Ak, bk, ck, d) mit d=c0 aus Gleichung (79) ergibt sich aus
![]()
4.4 Experimentelle Ergebnisse
Vorgangsweise nach [Mackenzie et al., 1997]:
- Ausgangspunkt sind die gemessenen HRTF-Impulsantworten (Kunstkopf) von 512 Samples bei 44,1 kHz.
- Entfernen der Zeitverzögerung am Anfang
- Diffusfeld-Entzerrung der HRTFs
- Glättung der Amplitudenantwort
- Rekonstruktion einer minimalphasigen Version => 128-Punkt-Antwort
- Interpretation der 128-Punkt-Antwort als FIR-Filter mit den Koeffizienten c0, c1, ... , cn.
- BMT wie in Abschnitt 4.3 beschrieben
In [Mackenzie et al., 1997] wurden IIR-Filter 10. Ordnung mittels BMT von FIR-Filtern 128. Ordnung eines HRTF-Satzes abgeleitet. Die Abbildung 17 zeigt die Amplitudenantworten für 19 HRTFs von FIR-Filtern 128. Ordnung (linke Seite) bzw. IIR-Filtern 10. Ordnung (rechte Seite). Die Autoren erhalten bessere Ergebnisse als mit nach der Prony- und Yule-Walker-Methode (wie sie in der Matlab-Toolbox implementiert sind) entworfenen IIR-Filtern (Abb. 18).
[Beliczinski et al., 1992] konnten folgende praktische Beobachtungen machen:
- Enge Bandpaßfilter konnten effizienter als breitere Bandpaßfilter desselben Phasentyps reduziert werden.
- Bei verschiedenen Filtern mit gleicher Amplitudenantwort wurde die beste Reduktion für minimalphasige Filter erzielt. Bei Maximalphasigkeit ergab sich eine signifikant schlechtere Reduktion.
- Die präsentierte Technik ist am geeignetsten für "nahezu linearphasiges" IIR-Filterdesign. Die effiziente Reduktion ist möglich, weil die Prototyp-FIR-Filter in der gesamten Bandbreite linear sind, die reduzierten IIR-Filter jedoch sind nichtlinear in den irrelevanten Stopbändern, behalten die Linearphasigkeit in den Durchlaßbändern aber bei.
4.5 Weitere mathematische Zusammenhänge
Zusatz 1
Dies ist (neben der Bestimmung der Hankel-Singulärwerte in Abschnitt 4.2 und 4.3) eine
weitere Möglichkeit zur Bestimmung einer balancierten Realisierung.
Man bestimmt nun eine spezielle Transformation T durch die Matrizen S, U und å, die zu einer balancierten Realisierung führt. Es gilt:
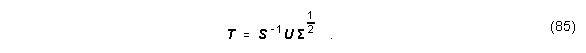
Dabei sind die Matrizen S, U und durch folgende Zusammenhänge gegeben:
Wenn das System (A, b, c) stabil ist und außerdem steuerbar und beobachtbar, dann sind die Matrizen P und Q positiv-definit und können faktorisiert werden:
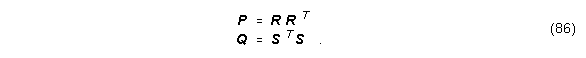
Dann ist die Matrix
![]()
eine symmetrische Matrix, die folgendermaßen faktorisiert werden kann:
![]()
wobei
![]()
Daß diese Wahl von T tatsächlich auf eine balancierte Realisierung führt, zeigt folgende Umformung:
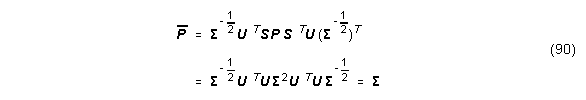
und
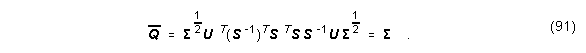
Die Transformation T, auf das System (A, b, c) angewandt, ergibt also ein balanciertes System.
Eine balancierte Realisierung ist eindeutig bezüglich einer beliebigen Zustandsraumtransformation Tb, wenn gilt
![]()
Zusatz 2
Die Hankel-Matrix kann geschrieben werden als
![]()
wobei
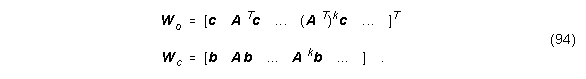
Das Kronecker-Theorem besagt, daß der Rang (H) gleich der Ordnung von F(z) ist. Nachdem Gl. (57) so geschrieben werden kann
![]()
ist
![]()
Analog kann man zeigen, daß
![]()
Die Matrizen Wo und Wc definiert in Gleichung (94) haben ebenfalls endliche Dimensionen:
![]() ist die Menge reeller Matrizen, Wo bzw. Wc wird Beobachtbarkeits- bzw. Steuerbarkeitsmatrix genannt.
ist die Menge reeller Matrizen, Wo bzw. Wc wird Beobachtbarkeits- bzw. Steuerbarkeitsmatrix genannt.
Zusatz 3
Folgesatz:
Für das oben angeführte System (A, b, c) sind die Steuerbarkeitsmatrix und die
Steuerbarkeits-Gramsche Matrix Einheitsmatrizen, das heißt
![]()
Zusatz 4
In Übereinstimmung mit den Gleichungen (93), (98), (97) und (73) sind
![]()
und
![]()
sowie
![]()
Zusatz 5
Theorem:
Ist die Hankel-Matrix H eines FIR-Filters (A, b, c) n-ter Ordnung (nach Gl. (101)) wie in
Gleichung (73) faktorisiert, dann ist ein reduziertes balanciertes System k-ter Ordnung
Eingangs-/Ausgangs-äquivalent zum System (Ak, bk, ck), wobei
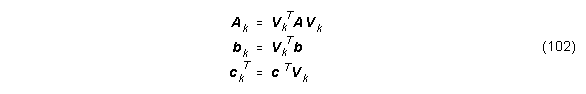
und Vk eine rechteckige n×k-Matrix ist, erhalten durch die folgenden Partitionierung:
![]()
Beweis:
Partitioniert man L wie folgt
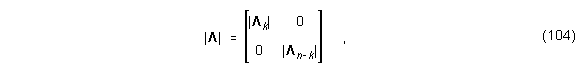
dann erhält man unter Verwendung der Zustandstransformation die balancierte Realisierung
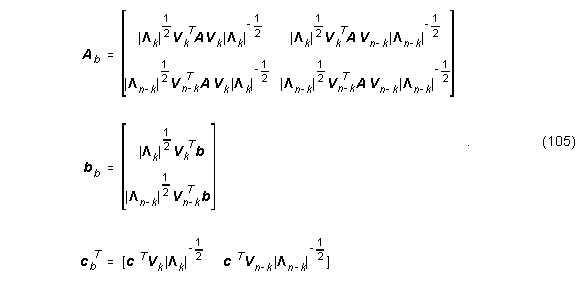
Das gestutzte System hat dann die Übertragungsfunktion
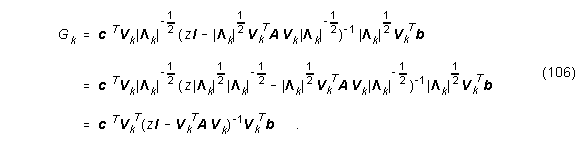
Aufgrund der speziellen Form von A und b kann man zeigen, daß
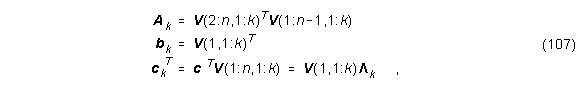
wobei V(i:j, k:m) die Extraktion der Reihen i bis j und der Spalten k bis m der Matrix V bedeutet.
1. tr A ist die Spur (trace) der Matrix A. Sie ist definiert als die Summe der Elemente in der Hauptdiagonale von A und ist weiters gleich der Summe der Eigenwerte von A.
2. Beweis: Unter Verwendung der Gleichungen (81) und (94) erhält man (98).
Quellenverzeichnis
Beliczynski B., Kale I., Cain G. D. (1992): "Approximation of FIR by IIR Digital Filters: An Algorithm Based on Balanced Model Reduction", IEEE Transactions on Signal Processing, vol. 40, no. 3, pp. 532-542.Brandenstein H., Unbehauen R. (1998): "Least-Squares Approximation of FIR by IIR Digital Filters", IEEE Transactions on Signal Processing, vol. 46, no. 1, January 1998, pp 21-30.
Chen J., Van Veen B. D., Hecox K. E. (1992): "External ear transfer function modeling: A beamforming approach", Journal of the Acoustical Society of America, 92(4), Pt. 1, pp. 1933- 1944.
Chen J., Van Veen B. D., Hecox K. E. (1995): "A spatial feature extraction and regularization model for the head-related transfer function", Journal of the Acoustical Society of America, 97(1), pp. 439-452.
Gersho A., Gray R. M. (1992): "Vector Quantization and Signal Compression", Kluwer Academic Publishers, Boston/Dordrecht/London, 1992.
Jot J.-M., Larcher V., Warusfel O. (1995): "Digital Signal Processing Issues in the Context of Minaural and Transaural Stereophony", Preprint 3980 of the 98th Audio Engineering Society Convention, Paris, Februar 1995.
Kale I. (1993): "High Fidelity Digital Filter Design and Implementation Techniques", ERK ´93, Portoro
Kistler D. J., F. L. Wightman (1992): "A model of head-related transfer functions based on principal components analysis and minimum phase reconstruction", Journal of the Acoustical Society of America, 91(3), pp. 1637-1647.
Ludyk G. (1995): "Theoretische Regelungstechnik 1+2", Springer Verlag Berlin Heidelberg, 1995
Mackenzie J., Huopaniemi J., Välimäki V., Kale I. (1997): "Low-Order Modeling of Head- Related Transfer Functions Using Balanced Model Truncation", IEEE Signal Processing Letters, vol. 4, no. 2, pp. 39-41.
Marolt M. (1996): "A New Approach to HRTF Audio Spazialization", Proceedings of the International Computer Music Conference 1996, pp. 365-367, San Francisco, International Computer Music Association.
Middlebrooks J. C., Green D. M. (1992): "Observations on a principal components analysis of head-related transfer functions", Journal of the Acoustical Society of America, 92(1), pp. 597- 599.
Oppenheim A. V., Shafer R. W.: "Discrete-Time Signal Processing", Prentice Hall, 1989.
Wu Z., Chan F. H. Y., Lam F. K., Chan J. C. K. (1997): "A time domain binaural model based on spatial feature extraction for the head-related transfer function", Journal of the Acoustical Society of America, 102(4), pp. 2211-2218.
© 2000 zuletzt geändert am 26. Jänner 2000.

