IEM-Report 09/99 Ambisonic System mit unsymmetrischem Lautsprecher Layout
Probleme bei unsymmetrischen Lautsprecherlayouts und der Versuch diese zu kompensieren.
Bei der Bestimmung eines Ambisonic Systems steht zu Beginn die Wahl der Dimension (2 oder 3-dimensional) und der Ordnung (1., 2. oder höhere Ordnung). Diese Wahl legt die Anzahl der Kanäle aber auch implizit die minimale Anzahl der Lautsprecher fest [1], [2]. Eine Monoquelle aus Richtung (j ,q) mit dem Signal S wird allgemein für ein 3-dim. System 1.Ordnung in folgender Form in die entsprechenden Kanäle kodiert: (Gleichungen 1-4)Kodierungsvorschrift:
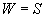
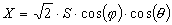
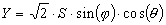
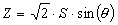 Die dazu gehörigen Lautsprechersignale für eine "symmetrische" Anordnung (Subscript n, für den n-ten Lautsprecher an der Position (j
n,qn) ) berechnen sich aus der Formel (Gleichung 5):
Die dazu gehörigen Lautsprechersignale für eine "symmetrische" Anordnung (Subscript n, für den n-ten Lautsprecher an der Position (j
n,qn) ) berechnen sich aus der Formel (Gleichung 5):
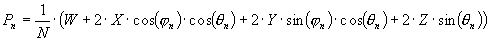 mit N = Anzahl der Lautsprecher
Bei Lautsprecherlayouts von Ambisonic Systemen werden grundsätzlich 2 Fälle unterschieden: symmetrische und unsymmetrische Anordnung. Liegen alle Lautsprecher auf einer gemeinsamen Kugeloberfläche1 und sind diese "gleichverteilt" (Winkelauflösung ist konst.) so handelt es sich um eine symmetrische Anordnung. Um eine einheitliche Behandlung beider Fälle zu gewährleisten, führt man eine Parametrisierung (a
, b
, g
, d
) durch. Dadurch werden die "matching conditions" (Gleichungen 7-10) auch für unsymmetrische Anordnungen erfüllt. Diese "matching conditions" ergeben sich aus der Annahme, daß es sich bei den ausbreitenden Wellen um "Ebene Wellen" handelt. Die Ebene Welle läßt sich in einer Reihe von mit Besselfunktionen gewichteten Cosinus-Schwingungen darstellen [2].
mit N = Anzahl der Lautsprecher
Bei Lautsprecherlayouts von Ambisonic Systemen werden grundsätzlich 2 Fälle unterschieden: symmetrische und unsymmetrische Anordnung. Liegen alle Lautsprecher auf einer gemeinsamen Kugeloberfläche1 und sind diese "gleichverteilt" (Winkelauflösung ist konst.) so handelt es sich um eine symmetrische Anordnung. Um eine einheitliche Behandlung beider Fälle zu gewährleisten, führt man eine Parametrisierung (a
, b
, g
, d
) durch. Dadurch werden die "matching conditions" (Gleichungen 7-10) auch für unsymmetrische Anordnungen erfüllt. Diese "matching conditions" ergeben sich aus der Annahme, daß es sich bei den ausbreitenden Wellen um "Ebene Wellen" handelt. Die Ebene Welle läßt sich in einer Reihe von mit Besselfunktionen gewichteten Cosinus-Schwingungen darstellen [2].
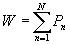
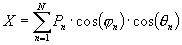
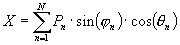
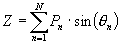 Mit den allgemeinen Lautsprechersignalen (loudspeaker feeds):
Mit den allgemeinen Lautsprechersignalen (loudspeaker feeds):
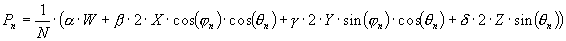
matching conditions:
Anhand einer speziellen Vorgabe wird nun die Vorgangsweise dokumentiert.
Geg.: 2 Lautsprecherkreise, mit je 30m Durchmesser, á 8 Lautsprecher (gleichmäßig verteilt) übereinander (Höhendifferenz 4m) angeordnet.
Es handelt sich hierbei um eine unsymmetrische Anordnung, da die Winkelauflösung bzgl. der Elevation nicht gleichmäßig erfolgt. Da es sich um eine 3-dim. Anordnung handelt, stellt sich nur noch die Frage der Ordnung des Systems. Gerzon hat in seinem "Metatheory"-Artikel [3] bewiesen, daß für ein Ambisonic-System mit 4 Lautsprechern im Rechteck die Verwendung von 3 Signalen, nämlich W,X und Y hinreichend ist. Er hat festgestellt, daß durch die Verwendung eines vierten Signales die Abbildungsfehler zunehmen (Vgl. auch Bamfords Arbeit). Weiters findet sich in der Literatur die Aussage, daß bei Ambisonic-Systemen immer mindestens soviele Lautsprecher zur Verfügung stehen müssen wie Übertragungskanäle. Das heißt für ein horizontales (=2-dimensionales) System müssen 3 LS für 1. Ordnung und 5 LS für 2. Ordnung zur Verfügung stehen. Frage: Ist es möglich, bei einer wie oben gegebenen Lautsprecheranordnung (siehe Geg.:), ein Ambisonic System 1.Ordnung in der Horizontalebene, aber ein System 2.Ordnung in der Vertikalen, um trotz des geringen Abstands zwischen den Lautsprecher-Ringen einen verbesserten Höheneindruck zu erreichen? Erklärung: Man nehme vier LS an den Positionen (x,y), (x,-y), (-x,y) und (-x,-y) im Rechteck. Es sei x > y, d.h. Das Rechteck hat vorne und hinten eine Schmalseite. Für die Konfiguration sind W,X und Y als Signale ausreichend, die Abbildung in y- Richtung wird schlechter sein als in x-Richtung, da die LS nicht weit genug auseinander stehen. Ein System 2.Ordnung könnte in seiner Gesamtheit nicht realisiert werden, ohne den Abbildungsfehler zu erhöhen. Wohl wäre es theoretisch möglich z.B. nur eine Komponente der 2. Ordnung, sin(2j ), als 4. Signal hinzuzufügen, doch das erhöht den "Wave Front Mismatch Error" und den absoluten Fehler. Wenn jetzt dieses LS-Rechteck um die y-Achse zu drehen beginnt, so wird die z-Koordinate miteinbezogen. Die 4 LS beschreiben bei dieser Drehung zwei Ringe mit den Mittelpunkten (0,y,0) und (0,-y,0), der Drehachse (0,1,0) und dem Radius x. Für den Anteil des Y-Signals zu den LS-Signalen hat die Rotation des LS-Rechtecks überhaupt keine Bedeutung. Er wäre immer gleich groß. Wenn man entlang der durch die Drehung entstandenen Ringe noch zusätzliche Lautsprecher setzt, so unterscheiden sich deren Signale natürlich in ihren X- und Z- Anteilen. Das ursprüngliche X-Signal wird hier aufgeteilt in zwei Medianebenen- Signale, nämlich X und Z. Wenn man die Anzahl der LS auf diesen Ringen erhöht, wird die Abbildung in der Medianebene sicher besser, die y-Abbildung und damit die Behandlung der Y-Signals bleiben davon unberührt. Es wirken also die zwei LS-Ringe für die y-Richtung so wie nur 4 LS. Wenn man diese LS-Konfiguration (zwei Ringe mit den Mittelpunkten (0,y,0) und (0,-y,0) und dem Radius x) nun um 90° um die x-Achse dreht, so erhält man die oben vorausgesetzte LS-Situation. Die y-Achse und die z-Achse wurden dadurch getauscht. Es wirken also die 2 LS-Ringe für die Abbildung in die Vertikale so wie 4 LS an den Stellen (x,z), (x,-z), (-x,z) und (-x,-z). Daher ist ein vertikales System 2. Ordnung nicht zielführend. Somit wählt man ein System 1.Ordnung. Durch die gegebene Lautsprecheranordnung ergibt sich für die Höhenauflösung (Vertikalkomponente) eine gewisse Einschränkung, die durch eine Parametrisierung "kompensiert" werden kann.Berechnung der Parameter
Die Berechnung der Parameter a , b , g und d erfolgt mit Hilfe der "matching conditions" (Gleichungen 6 bis 9) und der Formel für die Lautsprechersignale (Gleichung 10). Es ergeben sich für die Anordnung folgende Parameter für die Lautsprechersignale: a = 1 b = 0.67852 g = 0.67852 d = 19.0836 Bedingt durch das Lautsprecherlayout ergibt sich eine symmetrische Parametrisierung bezüglich X und Y. Da der Elevationswinkel 2q n, den die beiden Ringe einschließen, sehr klein ist, kommt es zu einem sehr großen Parametrisierungswert d für den Z-Kanal. Man erhält das vorläufige Ergebnis der Dekodiermatrix, welches in der folgenden Tabelle (Tabelle 1) dargestellt ist.Tabelle 1:
|
LS |
azmuth in [ °] |
elevation in [ °] |
W |
X |
Y |
Z |
|
|
Ring 1 |
|||||||
|
1 |
0 |
-7.5946 |
0.0625 |
0.1261 |
0.0000 |
-0.4729 |
|
|
2 |
45 |
-7.5946 |
0.0625 |
0.0892 |
0.0892 |
-0.4729 |
|
|
3 |
90 |
-7.5946 |
0.0625 |
0.0000 |
0.1261 |
-0.4729 |
|
|
4 |
135 |
-7.5946 |
0.0625 |
0.0892 |
0.0892 |
-0.4729 |
|
|
5 |
180 |
-7.5946 |
0.0625 |
0.1261 |
0.0000 |
-0.4729 |
|
|
6 |
225 |
-7.5946 |
0.0625 |
-0.0892 |
-0.0892 |
-0.4729 |
|
|
7 |
270 |
-7.5946 |
0.0625 |
0.0000 |
-0.1261 |
-0.4729 |
|
|
8 |
315 |
-7.5946 |
0.0625 |
0.0892 |
-0.0892 |
-0.4729 |
|
|
Ring 2 |
|||||||
|
9 |
0 |
7.5946 |
0.0625 |
0.1261 |
0.0000 |
0.4729 |
|
|
10 |
45 |
7.5946 |
0.0625 |
0.0892 |
0.0892 |
0.4729 |
|
|
11 |
90 |
7.5946 |
0.0625 |
0.0000 |
0.1261 |
0.4729 |
|
|
12 |
135 |
7.5946 |
0.0625 |
-0.0892 |
0.0892 |
0.4729 |
|
|
13 |
180 |
7.5946 |
0.0625 |
-0.1261 |
0.0000 |
0.4729 |
|
|
14 |
225 |
7.5946 |
0.0625 |
-0.0892 |
-0.0892 |
0.4729 |
|
|
15 |
270 |
7.5946 |
0.0625 |
0.0000 |
-0.1261 |
0.4729 |
|
|
16 |
315 |
7.5946 |
0.0625 |
0.0892 |
-0.0892 |
0.4729 |
|
Große Parametrisierungsfaktoren führen zu einer gegenphasigen Ansteuerung der Lautsprecher für Signale aus der entsprechenden Richtung (hier die Z-Richtung). Durch die gegenphasige Ansteuerung wird zwar die "Stereobreite", hier die Ausdehnung in der Z-Richtung, vergrößert, jedoch kommt es zu einem unerwünschten Nebeneffekt. Dieser Effekt ist auch bei Stereoabbildungen bzw. bei der Vergrößerung der Stereobreite bekannt als "phasiness". Gerzon zeigt in [4] eine mögliche Berechnung.
Berechnung bzw. Bestimmung der "phasiness":
In [4] bezeichnet Gerzon die Känale entsprechend der Stereoapplikationen mit L und R. Für ein Signal aus q = 90° (X=Y=0) erhält man für den oberen LS-Ring das Signal O (anstelle von L) und für den unteren Ring das Signal U (anstelle von R).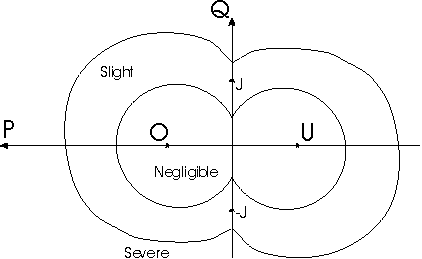 hier: (für
hier: (für - Das Ambisonic-Signal wird selbst kodiert. Wenn das Ambisonic Signal selbst kodiert wird, kann man den phasiness Effekt dahingehend vermeiden, indem man den zu kodierenden Winkel komprimiert. Das Ambisonic Signal muß vor der Encodierung entsprechend modifiziert werden. Diese Modifikation kann durch eine entsprechende Winkelkompression bezüglich der Z-Komponente erfolgen (siehe Abbildung 2). Somit ergibt sich für die Gleichung (4) eine Modifizierung wie folgt:
- Das Ambisonic-Signal liegt kodiert vor.
 (15)
(15) 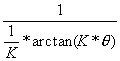 hier: K = 7.65
hier: K = 7.65
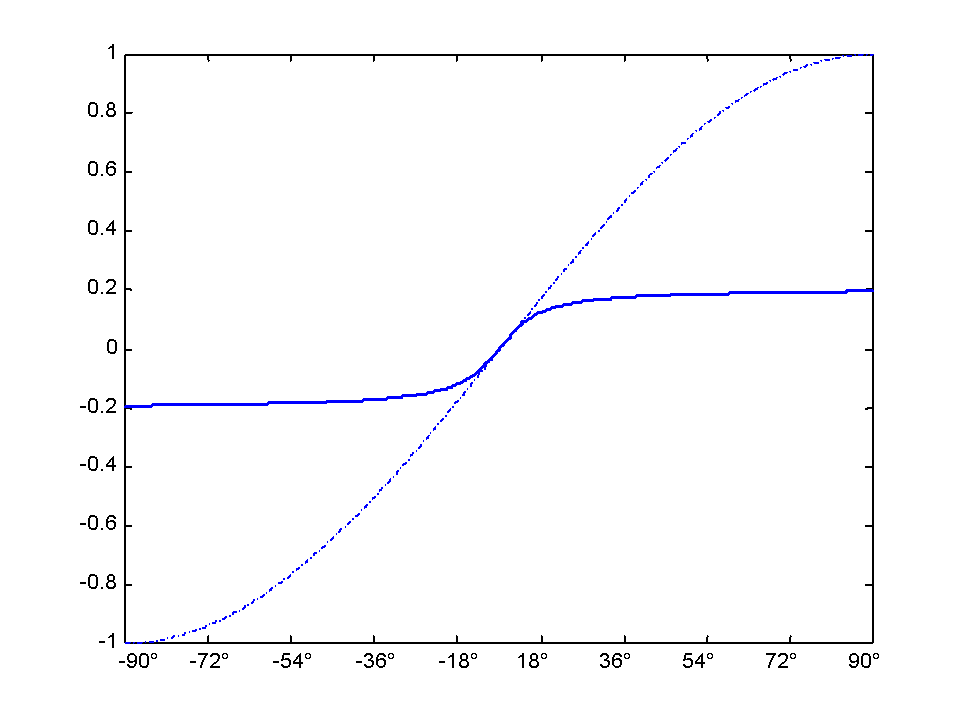
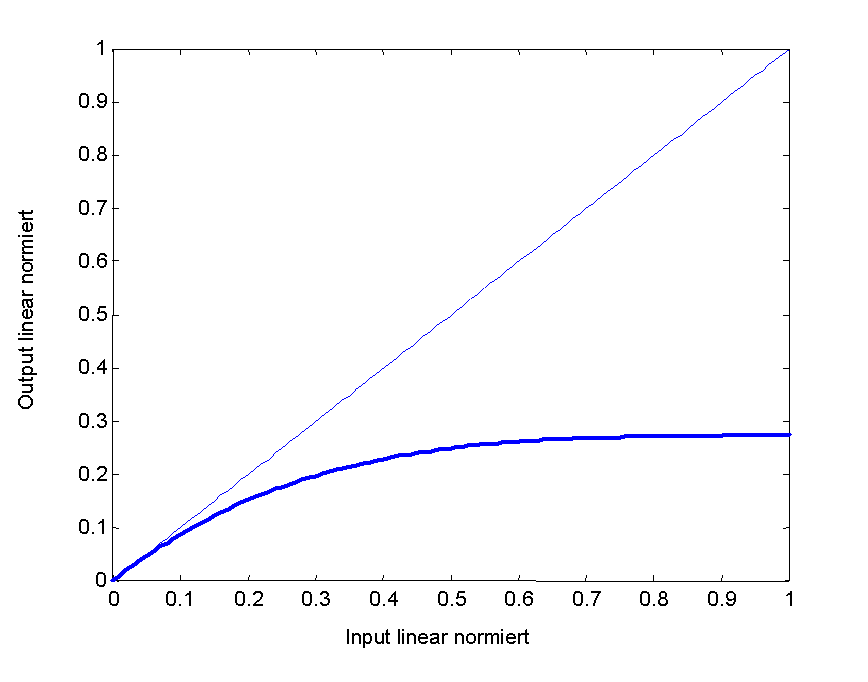
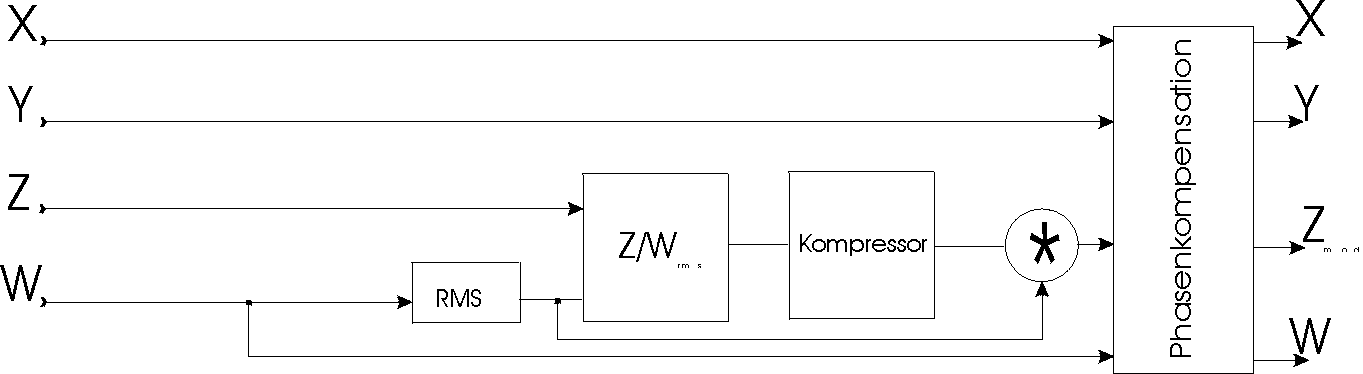 Die in Abbildung 3 dargestellte Vorgangsweise benötigt einen Kompressor, der eine Kennlinie besitzt, die in Abbildung 4 dargestellt ist (mit A = 5.14 bzw. -11.2dB).
Die in Abbildung 3 dargestellte Vorgangsweise benötigt einen Kompressor, der eine Kennlinie besitzt, die in Abbildung 4 dargestellt ist (mit A = 5.14 bzw. -11.2dB).
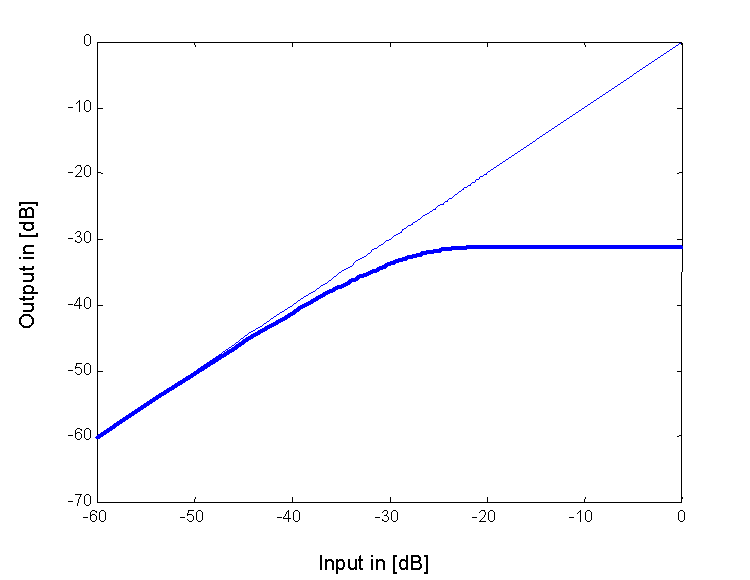
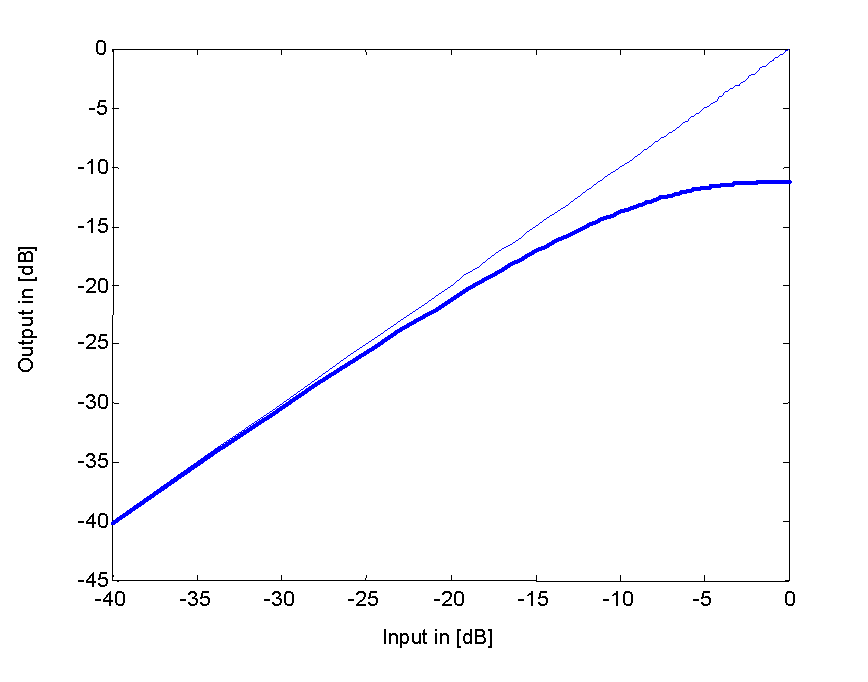 Da der oben angeführte Fall nur durch zusätzliche programmierbare Hardware realisierbar ist, stellt sich die Frage nach einer einfachen praktischen Lösung. Eine einfache Lösung stellt die alleinige Kompression des Z-Kanals dar. Damit man auch hier die entsprechende Kompressionskennlinie bestimmen kann, wird bei dieser Vorgangsweise von einer "mittleren Aussteuerung" von –20dB ausgegangen. Der Abschwächungsfaktor A wird auch hier in einen dB-Wert umgerechnet und bestimmt damit die Kompressorkennlinie (siehe Abbildung 5).
Da der oben angeführte Fall nur durch zusätzliche programmierbare Hardware realisierbar ist, stellt sich die Frage nach einer einfachen praktischen Lösung. Eine einfache Lösung stellt die alleinige Kompression des Z-Kanals dar. Damit man auch hier die entsprechende Kompressionskennlinie bestimmen kann, wird bei dieser Vorgangsweise von einer "mittleren Aussteuerung" von –20dB ausgegangen. Der Abschwächungsfaktor A wird auch hier in einen dB-Wert umgerechnet und bestimmt damit die Kompressorkennlinie (siehe Abbildung 5).
 Der Vorteil dieser Methode beruht in der relativ leichten Handhabung. Als Nachteil erscheint hier jedoch die Behandlung von leisen Signalen, die aus dem Richtungsbereich q
= 90° kommen, sowie die von lauten Signalen, deren Höhenauflösung dadurch verschlechtert wird.
Referenzen:
Der Vorteil dieser Methode beruht in der relativ leichten Handhabung. Als Nachteil erscheint hier jedoch die Behandlung von leisen Signalen, die aus dem Richtungsbereich q
= 90° kommen, sowie die von lauten Signalen, deren Höhenauflösung dadurch verschlechtert wird.
Referenzen:
[1] M. A. Gerzon, "Periphony: With-heigth Sound Reproduction" J. Audio Eng. Soc., Vol. 21, pp. 2-10, 1973, January.
[2] J. S. Bamford, "An Analysis of Ambisonic Sound Systems of First and Second Order", Thesis presented to the University of Waterloo, Waterloo, Ontario, Canada, 1995 [3] M. A. Gerzon, "General Metatheory of Auditory Localisation", Preprinted at the 92nd Audio Engineering Convention 1992, March, Vienna.[4] M. A. Gerzon, Signal Processing for Simulating Realistic Stereo Images, 93rd AES Convention 1992, October, San Francisco.
---------------------------
1 Liegen die physikalischen Lautsprecher aus der Sicht des Zentralhörers nicht auf einer gemeinsamen Kugeloberfläche, so müssen deren Abweichungen mit entsprechenden Zeitverzögerungsglieder kompensiert werden.
© 2000 zuletzt geändert am 8. Februar 2000.

